Question

A series LCR circuit containing a resistance of $120\Omega$ has angular frequency $4\times {{10}^{5}}rad{{s}^{-1}}$. At resonance the voltage across resistance and inductance are 60V and 40V respectively. The angular frequency at which the current in the circuit lags the voltage by $\dfrac{\pi }{4}$ is –

& \text{A) 2}\times {{10}^{5}}rad{{s}^{-1}} \\\ & \text{B) 6}\times {{10}^{5}}rad{{s}^{-1}} \\\ & \text{C) 8}\times {{10}^{5}}rad{{s}^{-1}} \\\ & \text{D) 10}\times {{10}^{5}}rad{{s}^{-1}} \\\ \end{aligned}$$

Answer 1

Hint : We need to find the relation between the resistance involved in the series LCR circuit and the resonance condition. The resonance conditions for voltage across the resistor and inductor can be used to solve this problem easily.

Complete answer:
We are given a series LCR circuit which includes a resistor, a capacitor and an inductor.

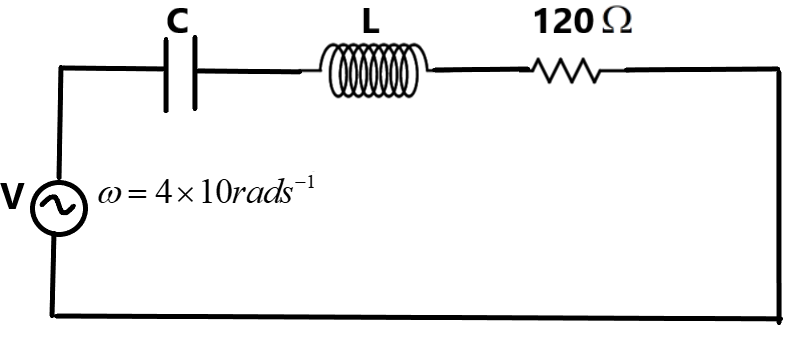
It is said that at the resonance condition a voltage drop of 60 V is measured across the resistor and 40V across the inductor. We know that in a LCR, during the resonance the complete voltage drop is across the resistor. The voltage drops across the inductor and the capacitor cancels off. So –

& {{V}_{R}}=60V \\\ & {{V}_{L}}=40V \\\ & {{V}_{C}}=-40V \\\ \end{aligned}$$ From this and the resistance value, we can find the current in the circuit as – $$\begin{aligned} & I=\dfrac{{{V}_{R}}}{R} \\\ & \Rightarrow I=\dfrac{60}{120} \\\ & \therefore I=0.5A \\\ \end{aligned}$$ Now, we can find the capacitive reactance and the inductive reactance using this current as – $$\begin{aligned} & {{X}_{L}}=\omega L \\\ & \text{but,} \\\ & {{X}_{L}}=\dfrac{{{V}_{L}}}{I} \\\ & \Rightarrow {{X}_{L}}=\dfrac{{{V}_{L}}}{I}=\omega L \\\ \end{aligned}$$ $$\Rightarrow {{X}_{L}}=\dfrac{40}{0.5}$$ $$\therefore {{X}_{L}}=80\Omega $$ $$\begin{aligned} & {{X}_{C}}=\dfrac{1}{C\omega }=\dfrac{{{V}_{C}}}{I} \\\ & \therefore {{X}_{C}}=80\Omega \\\ \end{aligned}$$ From these we can find the inductance and the capacitance as – $$\begin{aligned} & {{X}_{L}}=\omega L \\\ & \Rightarrow L=\dfrac{80}{4\times {{10}^{5}}} \\\ & \therefore L=0.2mH \\\ \end{aligned}$$ $$\begin{aligned} & {{X}_{C}}=\dfrac{1}{C\omega } \\\ & \Rightarrow C=\dfrac{1}{80\times 4\times {{10}^{5}}} \\\ & \therefore C=0.03125\mu F \\\ \end{aligned}$$ We know that in case of a series LCR circuit, the current lagging by $${{45}^{0}}$$ can be used to find the angular velocity by using the values of the resistance, inductance and capacitance as – $$\begin{aligned} & \tan \phi =\dfrac{{{X}_{L}}-{{X}_{C}}}{R} \\\ & \text{given, }\phi \text{=4}{{\text{5}}^{0}} \\\ & \Rightarrow \tan {{45}^{0}}=\dfrac{\omega L-\dfrac{1}{\omega C}}{R} \\\ & \Rightarrow R=\omega L-\dfrac{1}{\omega C} \\\ & \Rightarrow 120=\omega (2\times {{10}^{-4}})-\dfrac{1}{\omega (3.125\times {{10}^{-8}})} \\\ & \Rightarrow (2\times {{10}^{-4}}){{\omega }^{2}}-(32\times {{10}^{6}})-120\omega =0 \\\ & \Rightarrow {{\omega }^{2}}-(6\times {{10}^{5}})\omega -(1.6\times {{10}^{11}})=0 \\\ & \omega =\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\\ & \Rightarrow \omega =\dfrac{-(6\times {{10}^{5}})\pm \sqrt{{{(-6\times {{10}^{5}})}^{2}}-4(-1.6\times {{10}^{11}})}}{2} \\\ & \Rightarrow \omega =(3\times {{10}^{5}})\pm \dfrac{1}{2}\sqrt{3.6\times {{10}^{11}}+6.4\times {{10}^{11}}} \\\ & \Rightarrow \omega =(3\times {{10}^{5}})\pm \dfrac{1}{2}{{10}^{6}} \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow \omega =(3\times {{10}^{5}})\pm (5\times {{10}^{5}}) \\\ & \therefore \omega =(8\times {{10}^{5}})rad{{s}^{-1}} \\\ \end{aligned}$$ So, the angular frequency observed in the circuit when the current is lagging in the circuit is double the angular frequency at the resonance condition. **The correct answer is option C.** **Note:** The series LCR circuit has energy loss due to the resistor in the circuit. We can’t maintain a constant energy in the circuit by applying the voltage once unlike the LC circuits which are characterised with the LC oscillations like the simple pendulum.