Question

A series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80mF, R = 40 Ω.

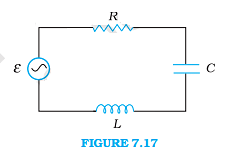
(a) Determine the source frequency which drives the circuit in resonance.

(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.

(c) Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency

Answer 1

Inductance of the inductor, L = 5.0 H Capacitance of the capacitor, C = 80 µH = 80 × 10−6 F Resistance of the resistor, R = 40 Ω Potential of the variable voltage source, V = 230 V (a) Resonance angular frequency is given as:

$ωr=\frac{1}{√LC}=\frac{1}{√5X80X10^{-6}}=\frac{10^3}{20}=50 rad/s$

Hence, the circuit will come in resonance for a source frequency of 50 rad/s. (b) Impedance of the circuit is given by the relation:

$Z=\sqrt(R^2+(X_L-X_C)^2)$At resonance, $X_L=X_C,Z=R=40 Ω$

Amplitude of the current at the resonating frequency is given as:$I°=\frac{V°}{Z}$

Where, V°=Peak voltage = $√2V=I°=\frac{√2V}{Z}=\frac{√2×230}{40}=8.13 A$

Hence, at resonance, the impedance of the circuit is 40 Ω and the amplitude of the current is 8.13 A. (c) rms potential drop across the inductor,

(VL)rms=IxωrL Where,

$Irms=\frac{I°}{√2}=\frac{√2V}{√2Z}=\frac{230}{40}=\frac{23}{4}A=(VL)rms=\frac{23}{4}x50x5=1437.5V$

Potential drop across the capacitor:

$(V_c)rms=I=\frac{1}{w_rc}=\frac{23}{4}X\frac{23}{4}X\frac{1}{50X80X10^{-6}}=1437.5V=230V$

Potential drop across the resistor:

$(VR)rms=IR=\frac{23}{4}X40=230V$

Potential drop across the LC combination:

$VLC=I(X_L-X_C)$

At resonance, $X_L=X_C,V_LC=0$

Hence, it is proved that the potential drop across the LC combination is zero at resonating frequency.