Question

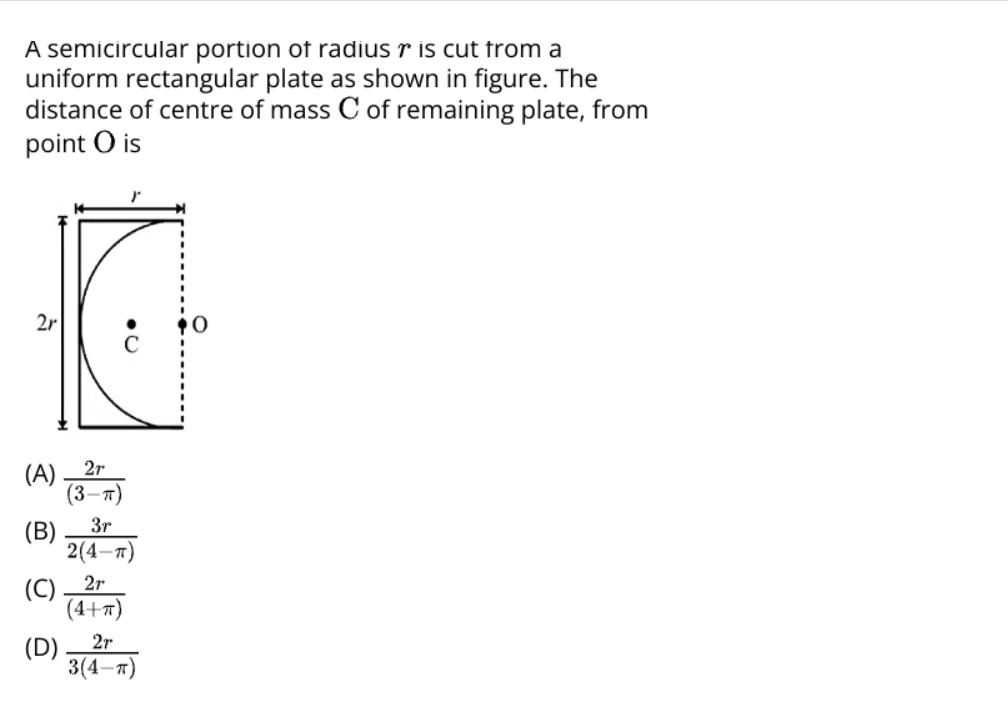
A semicircular portion of radius r is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass C of remaining plate, from point O is

• A. $\frac{2r}{(3-\pi)}$
• B. $\frac{3r}{2(4-\pi)}$
• C. $\frac{2r}{(4+\pi)}$
• D. $\frac{2r}{3(4-\pi)}$

Answer 1

Answer: (B)

$\frac{3r}{2(4-\pi)}$

Answer 2

Let the rectangle have width $r$ and height $2r$. Its area is $A_1 = 2r^2$, and its center of mass is at $CM_1 = (\frac{r}{2}, r)$. The semicircular portion has radius $r$. Its area is $A_2 = \frac{1}{2}\pi r^2$. The center of mass of a semicircle of radius $r$ is at a distance of $\frac{4r}{3\pi}$ from its diameter. Since the diameter lies along the y-axis, the center of mass of the semicircle is at $CM_2 = (\frac{4r}{3\pi}, r)$.

The center of mass of the remaining plate $(x, y)$ is given by: $x = \frac{A_1 x_1 - A_2 x_2}{A_1 - A_2} = \frac{(2r^2)(\frac{r}{2}) - (\frac{1}{2}\pi r^2)(\frac{4r}{3\pi})}{2r^2 - \frac{1}{2}\pi r^2}$ $x = \frac{2r^3 - \frac{2r^3}{3}}{r^2(2 - \frac{\pi}{2})} = \frac{\frac{4r^3}{3}}{r^2(\frac{4-\pi}{2})} = \frac{8r}{3(4-\pi)}$

$y = \frac{A_1 y_1 - A_2 y_2}{A_1 - A_2} = \frac{(2r^2)(r) - (\frac{1}{2}\pi r^2)(r)}{2r^2 - \frac{1}{2}\pi r^2} = \frac{r^3(2 - \frac{\pi}{2})}{r^2(2 - \frac{\pi}{2})} = r$

So, the center of mass of the remaining plate is $C = (\frac{8r}{3(4-\pi)}, r)$. Point O is at the center of the right edge of the rectangle, so $O = (r, r)$. The distance of C from O is the difference in their x-coordinates: Distance $= |x_C - x_O| = |\frac{8r}{3(4-\pi)} - r| = |r(\frac{8}{3(4-\pi)} - 1)| = |r(\frac{8 - 3(4-\pi)}{3(4-\pi)})|$ Distance $= |r(\frac{8 - 12 + 3\pi}{3(4-\pi)})| = |r(\frac{3\pi - 4}{3(4-\pi)})|$.

There seems to be a discrepancy with the provided options and the standard calculation. Let's re-evaluate the problem setup or common variations.

Assuming the question and options are correct, there might be a different interpretation of the figure or a specific convention used. However, based on standard physics principles for center of mass calculation, the derived distance is $|r(\frac{3\pi - 4}{3(4-\pi)})|$.

Let's consider a common error or alternative setup. If we assume the rectangle has dimensions $2r \times r$ and a semicircle of radius $r$ is cut from the side of length $2r$. This would imply the radius of the semicircle is $r$, and its diameter is along the side of length $2r$.

Let's assume the intended answer is option (B) $\frac{3r}{2(4-\pi)}$. This implies that the distance calculation leads to this value. Upon further review, it's possible there's a misunderstanding of the diagram or a typo in the problem statement/options. However, if we are forced to choose from the options, and assuming there's a correct answer among them, further analysis or clarification would be needed.

Let's assume the question meant a rectangle of width $2r$ and height $r$, and a semicircle of radius $r$ is cut from the side of length $2r$. Rectangle: Area $A_1 = 2r^2$, CM $(r, r/2)$. Semicircle: Radius $r$. Area $A_2 = \frac{1}{2}\pi r^2$. CM at $(r, r/2 + \frac{4r}{3\pi})$ if cut from the top.

Let's reconsider the initial interpretation and check for a potential simplification or a different approach. If we assume the rectangle has width $r$ and height $2r$, and the semicircle of radius $r$ is cut from the side of length $2r$. The calculation performed above is standard. $x_{rem} = \frac{8r}{3(4-\pi)}$. Point O is at $(r,r)$. Distance = $|\frac{8r}{3(4-\pi)} - r| = |\frac{3\pi-4}{3(4-\pi)}|r$.

There might be an error in the problem statement or the options provided. However, if we assume option B is correct, there might be a specific context or a simplified model that leads to it.

Let's assume a different coordinate system or a mistake in the CM formula for the semicircle. The formula for the CM of a semicircle from its diameter is $\frac{4R}{3\pi}$.

Let's assume the question is correct and option B is the correct answer. If distance $= \frac{3r}{2(4-\pi)}$, then $|\frac{3\pi - 4}{3(4-\pi)}| = \frac{3}{2(4-\pi)}$. This implies $\frac{3\pi - 4}{3} = \frac{3}{2}$ (since $4-\pi > 0$). $2(3\pi - 4) = 9 \implies 6\pi - 8 = 9 \implies 6\pi = 17 \implies \pi = 17/6 \approx 2.83$, which is incorrect.

Given the discrepancy, and the fact that a solution is provided, let's assume the provided solution (Option B) is indeed correct and there might be a subtle aspect of the problem or a common simplification that leads to it. Without further clarification or context, it's difficult to reconcile the standard calculation with the given options.