Question
Question: A semicircular arc of radius r and a straight wire along the diameter, both are carrying the same cu...
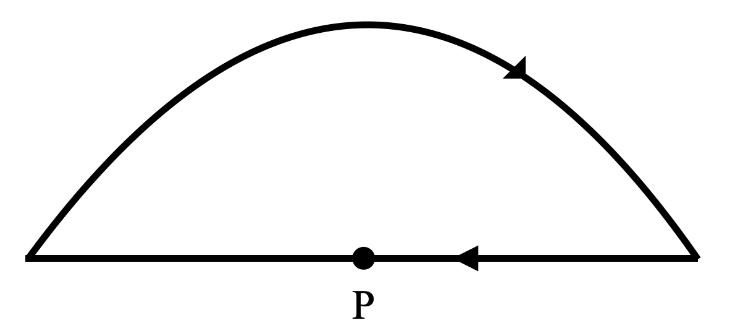
A semicircular arc of radius r and a straight wire along the diameter, both are carrying the same current i. Find out magnetic force per unit length on the small element P, which is at the centre of curvature?
A. (4rμ0i2)
B. (2rμ0i2)
C. (rμ0i2)
D. (r2μ0i2)
Solution
Hint: Biot-Savart’s law confirms that there won’t be any magnetic field at P due to the straight wire. Because, the point lies on the wire. We need to find the magnetic field at P due to the semicircular arc. We can find the force using the formula,
F=Bil
Where,
B is the magnetic field at that location
i is the current
l is the length of the wire.
Formula Used:
Magnetic field due to the semicircular arc,
B=4rμ0i
Where,
μ0 is the permittivity of the material
i is the current through the arc
r is the radius of the arc
Force per unit length is,
lF=Bi
Where,
B is the magnetic field
i is the current through the point
Complete step by step answer:
The radius of the semicircular arc is = r
Current passing through the loop = i
We can find the magnetic field due to a semicircular arc at the centre using Biot-Savart’s law. It is given by,
B=4rμ0i
Where,
μ0 is the permittivity of the material
i is the current through the arc
r is the radius of the arc
So, at point P the magnetic field is,
B=4rμ0i
Now, the current flowing through wire at P is i
The force per unit length due to the Magnetic field on a wire is,
lF=Bi...................(1)
Where,
F is the force on the wire
B is the magnetic field at that location
i is the current going through the wire
l is the length of the wire
So, in this case, the force per unit area will be given by,
lF=Bi
⇒lF=(4rμ0i)i
⇒lF=4rμ0i2
So, the magnetic force per unit length is
4rμ0i2
Hence, the correct option is (A).
Note: You can divide the entire loop into different segments. Find the magnetic field due to each segment. Don’t consider the segments which are aligned with the point at which we are finding the magnetic field. After that we can use the simple equation (1) to find force per unit length.
