Question

A semicircle is inscribed in a right angle triangle so that its diameter lies on the hypotenuse and the centre divides the hypotenuse into segments $15$ cm and $20$ cm long. Find the length of the arc of the semicircle included between its points of tangency with the legs.

Answer 1

Here, the semicircle is inscribed in a right angle triangle so that its diameter lies on the hypotenuse which means that the point that intersects the semicircle at two points lies outside the circle. And another line passes through this point which is tangent, then the power of the circle is given as- ${\text{(tangen}}{{\text{t}})^2} = {\text{product of the two points}}$

Complete step-by-step answer:

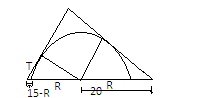
Let R be the radius of the semicircle and T be the tangent. Since the point through which the tangent passes and that intersects the semi-circle on two points lies outside the circle then the power of circle is-
$\Rightarrow$ ${\text{tangen}}{{\text{t}}^2} = {\text{product of the two points}}$ ${{\text{(T)}}^2}{\text{ = }}\left( {15 - {\text{R}}} \right)\left( {15 + {\text{R}}} \right)$=$225 - {{\text{R}}^2}$ --- (i)
Since the triangles are similar triangles, that is, same in shape but not in size so the ratio of corresponding sides of the triangles will be equal. Then we can write the ratio of radius to hypotenuse of right angled triangle is-
$\Rightarrow \dfrac{{\text{T}}}{{\text{R}}} = \dfrac{{15}}{{20}} = \dfrac{3}{4}$=k (let) --- (ii)
On solving the equation eq. (ii)
$\Rightarrow {\text{T = 3k and R = 4k}}$
On putting these values in eq. (i), we get-
$\Rightarrow {\left( {3{\text{k}}} \right)^2} = 225 - {\left( {4{\text{k}}} \right)^2}$ $\Rightarrow 9{{\text{k}}^2}{\text{ = 225 - 16}}{{\text{k}}^2}$
On separating the coefficients of k, we get-
$\Rightarrow \left( {16 + 9} \right){{\text{k}}^2} = 225 \Rightarrow 25{{\text{k}}^2} = 225 \\\ \Rightarrow {{\text{k}}^2} = \dfrac{{225}}{{25}} = 9 \\\$
$\Rightarrow {\text{k}} = 3$
On putting the value of k , we get,${\text{R = 12 and T = 9}}$
To find arc length, we use the given formula-
Arc length of quarter circle=$\dfrac{{\pi {\text{R}}}}{2}$
On putting the values, we get the arc length.
Arc length=$\dfrac{{\pi \times 12}}{2} = 6\pi$
Hence the arc length is $6\pi$ .

Note: The arc length of full circle is given by $\dfrac{{\pi {\text{R}}}}{4}$ as ${90^ \circ }$ is one quarter of a circle and 360 is full quarter. So to find the arc we change the formula to $\dfrac{{\pi {\text{R}}}}{2}$ .
Here, we have taken radius as hypotenuse because the radius of the circle lies on the hypotenuse.