Question

A semi-infinite insulating rod has linear charge density $\lambda$ . The electric field at the point P shown in figure is :-

(A) $\dfrac{{2{\lambda ^2}}}{{{{\left( {4\pi {\varepsilon _0}r} \right)}^2}}}$ at ${45^ \circ }$ with AB
(B) $\dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}{r^2}} \right)}}$ at ${45^ \circ }$ with AB
(C) $\dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}r} \right)}}$ at ${45^ \circ }$ with AB
(D) $\dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}r} \right)}}$ at perpendicular with AB

Answer 1

We will calculate the x-component and the y-component of the electric field at the point P, as shown in the figure, due to the semi-infinite insulating rod carrying uniform linear charge of density $\lambda$ .We integrate the electric field $d{E_x}$ over the length of the “semi-infinite” rod that is with respect to the variable $x$ from 0 to $\infty$ .

Complete step by step answer:
It has been given that a semi-infinite insulating rod has linear charge density $\lambda$ .

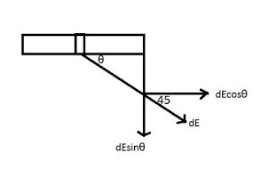
Consider an infinitesimal charge element of length $dx$ at distance $x$ from the end of the rod as shown in the figure.
$\cos \theta = \dfrac{x}{{\sqrt {{r^2} + {x^2}} }}$ by Pythagoras Theorem, which states that the square of the hypotenuse is equal to the square of the other two sides of a right angled-triangle.
As the direction of electric field due to a charge element is along the line joining the element to the point where the field is to be calculated.
From the figure, the x-component of the field will be,
$d{E_x} = dE\cos \theta$
$\Rightarrow d{E_x} = \dfrac{{\lambda dx}}{{\left( {{r^2} + {x^2}} \right)}} \times \dfrac{x}{{\sqrt {{r^2} + {x^2}} }}$
Integrating $d{E_x}$ over the length of the “semi-infinite” rod that is with respect to the variable $x$ from 0 to $\infty$ , we get
\int {d{E_x}} = k\lambda \int {\dfrac{{xdx}}{{{{\left( {{r^2} + {x^2}} \right)}^{{\raise0.7ex\hbox{ 3 } \\!\mathord{\left/ {\vphantom {3 2}}\right.} \\!\lower0.7ex\hbox{ 2 }}}}}}}
For simplicity we take $t = {r^2} + {x^2}$ .
Thus, $dxdx = dt$ .
On simplifying the equation, we can get,
\int {d{E_x}} = k\lambda \int {\dfrac{{dt}}{{{{\left( t \right)}^{{\raise0.7ex\hbox{ 3 } \\!\mathord{\left/ {\vphantom {3 2}}\right.} \\!\lower0.7ex\hbox{ 2 }}}}}}} .
By rules of integration,
\int {dE} = \dfrac{{k\lambda }}{2} \times \dfrac{{ - 3}}{2}{t^{ - {\raise0.7ex\hbox{ 1 } \\!\mathord{\left/ {\vphantom {1 2}}\right.} \\!\lower0.7ex\hbox{ 2 }}}} .
Substituting, the value of $t = {r^2} + {x^2}$ , and setting limits of integration at 0 and $\infty$ ,
$\int {d{E_x}} = k\lambda \left[ {\dfrac{1}{{\sqrt {{r^2} + {x^2}} }}} \right]_0^\infty$
$\Rightarrow {E_x} = \dfrac{{k\lambda }}{r}$
We note that $\left| {{E_x}} \right| = \left| {{E_y}} \right|$ for all $r$ .
Therefore, the angle that the electric field vector makes at P is
$\tan \theta = \dfrac{{\left| {{E_x}} \right|}}{{\left| {{E_y}} \right|}}$ .
Since $\left| {{E_x}} \right| = \left| {{E_y}} \right|$ , $\tan \theta = 1$ .
It implies that $\theta = {45^ \circ }$ and is independent of $r$ , that is the distance of the point P from the edge of the “semi-infinite” rod.
Now, the net electric field is given by, ${E_{net}} = \sqrt {{E_X}^2 + {E_Y}^2} = \sqrt 2 \dfrac{{k\lambda }}{r}$ where $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$ is a constant.
Hence the net electric field is $\dfrac{{\sqrt 2 \lambda }}{{\left( {4\pi {\varepsilon _0}r} \right)}}$ at ${45^ \circ }$ with AB.
The correct answer is Option C.

Note:
Electric field is defined as the electric force per unit charge. The direction of the field is taken to be the direction of the force it would exert on a positive test charge. The electric field is radially outward from a positive charge and radially in toward a negative point charge.