Question

A second harmonic has to be generated in a string of length l stretched between two rigid supports. The points where string has to be plucked and touched are
a)pluck at $l/4$ and touch at $3l/4$
b) pluck at $l/4$ and touch at $l/2$
c) pluck at $l/2$ and touch at $3l/4$
d) pluck at $l/2$ and touch at $l/4$

Answer 1

In the question it is clearly given to us that there is a string of length l fixed between two rigid supports. It is to be noted that we have touched a string where there is a node. And we have to pluck the sting at the place where we expect the maximum displacement of the string. Therefore considering this we will accordingly determine where the string has to be plucked and touched.
Formula used:
$P=\dfrac{l}{2n}$

Complete answer:

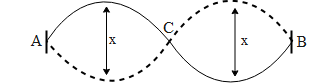
In the above figure we can see a string in the second harmonic. It is also called a second overtone. In the above figure we can also see that points A, B, and C represent the nodes. They are generally formed at the boundaries i.e. in the above figure at point A and B. Now in order to generate a second harmonic, we need to have two loops in the string. This is only possible if the middle point of the string is fixed i.e. it is touched. Therefore in the above figure i.e. point C we need to touch it. This point is exactly in the middle of the string so that we have two equal loops i.e. second harmonic.
Let us say the point where the string has to be plucked be P. Hence this point is given by $P=\dfrac{l}{2n}$where ‘n’ represents the particular harmonic of the string. Since we know n=2 we get,
$\begin{aligned} & P=\dfrac{l}{2n} \\\ & \Rightarrow P=\dfrac{l}{2(2)}=\dfrac{l}{4} \\\ \end{aligned}$
Therefore we can conclude that the string has to be plucked at $l/4$ and touched at $l/2$.

So, the correct answer is “Option B”.

Note:
One can actually determine the point of plucking and the touch by just looking at the above figure itself. The point C is fixed, from which we can imply that we have to touch it to keep fixed and since the string vibrates in the two segments of the string it has to be exactly at the middle. Now further since the string vibrates at its maximum between these two points we can imply we have to pluck it at exactly half the length with respect to the middle.