Question

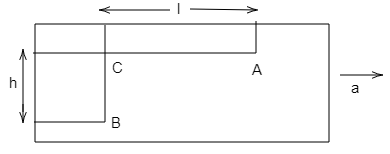
A sealed tank containing a liquid of density $\rho$ moves with horizontal acceleration $a$ as shown in the figure. The difference in pressure between two points $A$ and $B$ will be

$(A)h\rho g$
$(B)l\rho g$
$(C)h\rho g - l\rho a$
$(D)h\rho g + l\rho a$

Answer 1

This question is based on the concept of hydrostatic pressure. Hydrostatic pressure is the pressure exerted by or existing within a liquid at rest with respect to adjacent bodies. The SI unit of hydrostatic pressure is Pascal.

Complete answer:
In this question, we need to calculate the pressure difference between the two points $A$and $B$.
Now, since there is no height difference between $A$ and $C$, so no hydrostatic pressure difference between them. But, since the liquid is accelerating so there will be a pressure difference which will be created between them.
${P_C} - {P_A} = \rho al.........(1)$
Now, if we look at the two points $B$ and $C$, we can clearly see that the acceleration of both of them is the same as they are lying in the same vertical plane. But there is a height difference between these two points and thus, a hydrostatic pressure difference will be present between them.
${P_B} - {P_C} = \rho gh.........(2)$
On adding equation (1) and (2), we get,
${P_C} - {P_A} + {P_B} - {P_C} = \rho al + \rho gh$
${P_B} - {P_A} = \rho al + \rho gh$
Now, this equation can be rewritten as,
${P_B} - {P_A} = h\rho g + l\rho a$
So, the pressure difference between the points $A$ and $B$ is ${P_B} - {P_A} = h\rho g + l\rho a$.
Hence, the correct answer is $(D)h\rho g + l\rho a$.

Note: It is important to note that in such questions, there are two types of pressure difference. The first pressure difference is due to the hydrostatic pressure as the two points are at a different height. The other pressure difference is due to the fact that the liquid is accelerating horizontally.