Question

A screen is placed $90cm$ from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by $20cm$. Determine the focal length of the lens.

Answer 1

Hint: We will use a displacement method to find the focal length of the given convex lens. The distance of the object from the lens and that of the image from the lens can be interchanged and we would still get a focused image.

Formula used:
$f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}$

Complete step by step answer:
When the distance between object and screen is more than $4f$, we can obtain the image of the object on the screen for the two positions of the lens. It is known as the Displacement method.
Let’s consider the below figure,

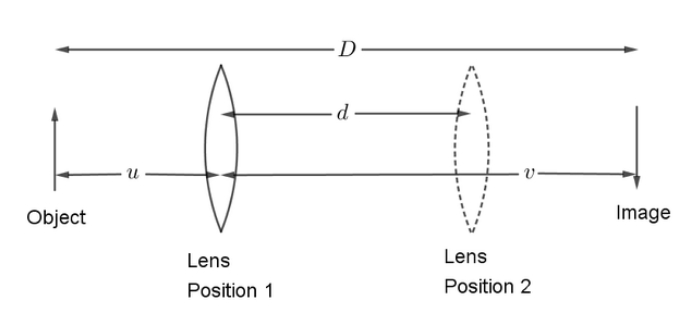
The convex lens is placed on a calibrated scale with the object at one end and a screen for obtaining the image at the other end.

The lens in first case is placed closer to the object and its position is adjusted so as to get a clear image on the screen. The position of the convex lens and the value of distance between the object and the image are noted.

With the same value of distance between the object and image, the lens is now moved towards the screen and its position is adjusted until a clear image of the object is obtained on the screen. This position of the lens is also noted.

Let the difference between the two positions of the lens for obtaining a clear image on the screen be$d$, and the distance between the object and the screen be $D$.

Repeat this for different distances between the object and the screen and note down the values of $D$ and the corresponding values of $d$.

Principle:
As per the principle of reversibility of light, if the direction of a ray of light is reversed, it will follow the same path as the original route.

Hence, the distance of the object from the lens and that of the image from the lens can be interchanged and we would still get a focused image.

Let the distance between the object and the lens be $u$and that between the image and the lens be $v$.
$D=u+v$
And, $d=v-u$
We get,
$v=\dfrac{D+d}{2}$
$u=\dfrac{D-d}{2}$
From the lens formula, we have,
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Where, $u,v,f$ are the distance of the object, image and focal length respectively.
The sign of $u$ is considered as negative and $v,f$ are positive for a real image.
Formula becomes,
$\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$
Putting the values of $u$ and $v$,
$\dfrac{2}{D+d}-\dfrac{2}{D-d}=\dfrac{1}{f}$
$\dfrac{4D}{{{D}^{2}}-{{d}^{2}}}=\dfrac{1}{f}$
We get,
$4f=\dfrac{{{D}^{2}}-{{d}^{2}}}{D}$
Or, $f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}$
Focal length of the lens is given by the formula, $f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}$
We are given,
Distance between object and screen, $D=90cm$
Distance between two locations of the lens, $d=20cm$
We have to calculate the focal length of convex lens
Using the formula,
$f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}$
Putting the values of $D$ and $d$, we get,
$\begin{aligned} & f=\dfrac{{{(90)}^{2}}-{{(20)}^{2}}}{4\times 90}=\dfrac{8100-400}{360} \\\ & f=\dfrac{7700}{360}=21.388 \\\ \end{aligned}$
$f=21.4cm$
Hence, the focal length of a convex lens is $21.4cm$.

Note: We see that the two positions of the convex lens for getting a clear and focused image of the object with constant value of distance between the object and image are symmetric. In other words, the distance between the object and the lens in the first position is the same as the distance between the image and the lens in the second position and also, the distance between the image and the lens in the first case or position is the same as the distance between the object and lens in the second position.