Question

A scooter going due east at $10\,{\text{m/s}}$ turns right through an angle of $90^\circ$ . If the speed of the scooter remains unchanged in taking this turn, the change in the velocity of the scooter is:
A. $20\,{\text{m/s}}$ in south-east direction
B. $17.5\,{\text{m/s}}$ in south-west direction
C. $10.0\,{\text{m/s}}$ in south-east direction
D. $14.14\,{\text{m/s}}$ in south-west direction

Answer 1

First, we will assign the vector components to the velocity and draw the diagram of it. We will find the change in velocity in vector form and then find the magnitude of it accordingly. Change means subtraction of final velocity from initial velocity.

Complete step by step answer:
In this problem, we are given that the velocity with which the scooter was moving due east was $10\,{\text{m/s}}$ .
It takes a right turn through an angle of $90^\circ$ .
While taking the turn the speed of the scooter remains unchanged i.e. it continues with the same velocity $10\,{\text{m/s}}$ . We are asked to find the change in velocity of the scooter along with the direction.

This problem can be explained by drawing diagrams, which makes it easier to understand. In the beginning, the direction of the scooter was due east and it took a right turn towards the south.
Let the component along the east direction be $\hat i$ and the component along the south direction be $- \hat j$ .

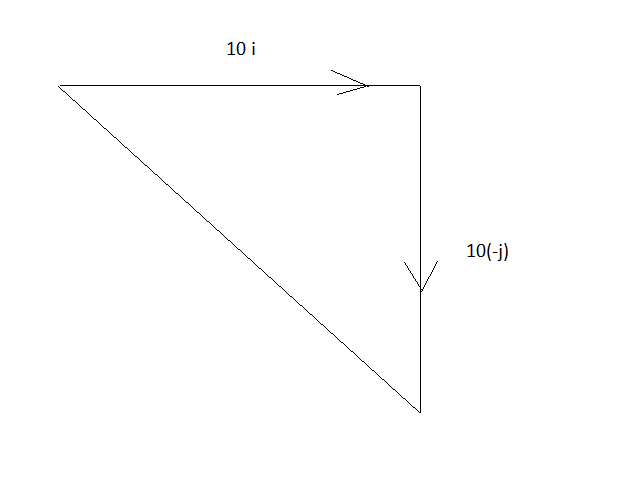
But we are asked to find the change in velocity, so we can write:
$\Delta v = {v_{\text{f}}} - {v_{\text{i}}}$ …… (1)
Where,
$\Delta v$ indicates change in velocity.
${v_{\text{f}}}$ indicates final velocity.
${v_{\text{i}}}$ indicates initial velocity.
Now, substituting the required values in equation (1), we get:

$$\Delta v = {v_{\text{f}}} - {v_{\text{i}}} \\\ \Delta v = - 10\hat j - 10\hat i \\\$$

From the above manipulation, it is clear that the $\hat i$ component gets reversed. So, we can add a new diagram, given below:

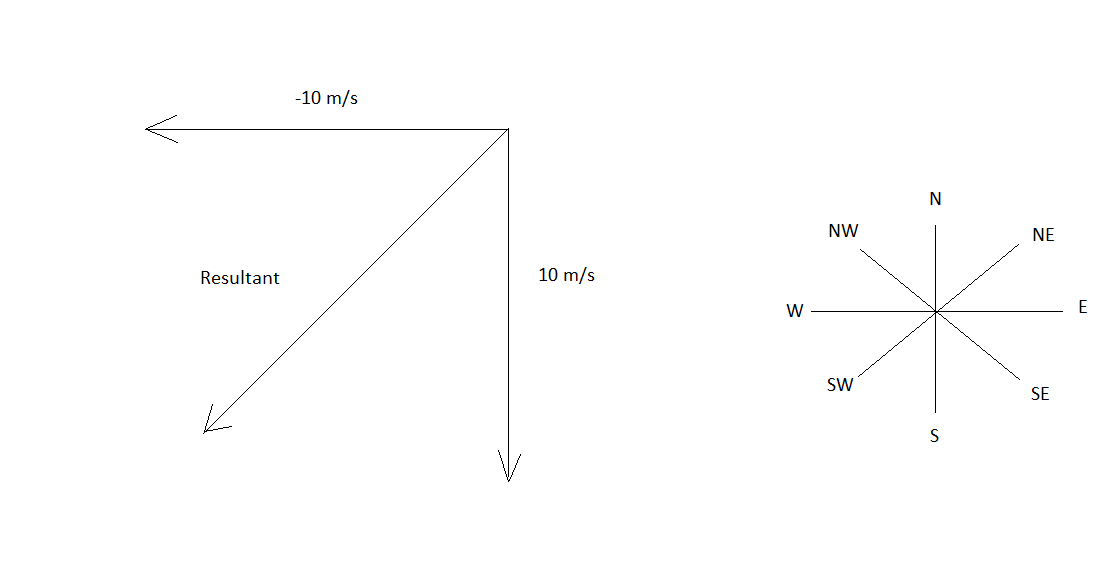
The direction of velocity which was due east previously, now becomes due south.
Now, we find the magnitude of the change in velocity:

$$\left| {\Delta v} \right| = \left| { - 10\hat j - 10\hat i} \right| \\\ \left| {\Delta v} \right| = \sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 10} \right)}^2}} \\\ \left| {\Delta v} \right| = 10\sqrt 2 \\\ \left| {\Delta v} \right| = 14.14\,{\text{m/s}} \\\$$

Hence, the magnitude of the change in velocity is $14.14\,{\text{m/s}}$ . The direction is south-west.

So, the correct answer is “Option D”.

Note:
While solving this problem, you should have a clear understanding of vectors. Most students make mistakes by not reversing the direction of velocity of the $\hat i$ component. The correct is $- \hat i$ component. Since, we are asked to find the change and change means subtraction. The negative sign of subtraction is of great significance, as it reverses the $\hat i$ component. Otherwise the direction will come south-east, which is not correct.