Question

A satellite of mass M is in a circular orbit of radius R about the centre of the earth. A meteorite of the same mass falling toward the earth, collides with the satellite completely elastically. The speed of the satellite and the meteorite just before collision are the same The subsequent motion of the combined body will be
a) in circular orbit of different radius
b) in a circular orbit of radius R
c) in an elliptical orbit
d) such that it escapes to infinity

Answer 1

It is given in the question the satellite and the meteorite collide completely in elastically. Hence its momentum will be conserved but its kinetic energy will not be conserved and will move together as a single body. The collision of the meteorite and the satellite should be taken at an angle of 90 since the satellite is moving in a circular orbit and the meteorite is moving towards the earth.

Complete answer: Let us consider the initial momentum of the satellite and the meteorite to be p = Mv where M is the mass of the meteorite as well as the satellite and v is also the same for both of them,

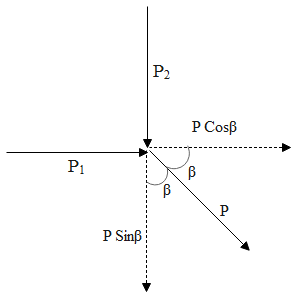
In the above diagram, ${{P}_{1}}$ is the momentum of the satellite orbiting the earth and is the momentum of the meteorite moving towards the earth. Their resultant is given by P by the laws of vector addition.
Using law of conservation of momentum,

${{P}_{1}}=P\operatorname{Cos}\beta \text{ and }{{P}_{2}}=P\operatorname{Sin}\beta$ Hence the magnitude of P is given as,
$P=\sqrt{{{P}_{1}}^{2}\text{ + }{{P}_{2}}^{2}}$ but we know ${{P}_{1}}={{P}_{2}}=Mv$ Hence we get
$P=\sqrt{2}Mv$ Since momentum in general is given as mass into velocity P can be written as,
$2MV=\sqrt{2}Mv$ where V is the velocity in the direction of resultant momentum and 2M is the mass of the satellite and the meteorite moving together.

Hence the resultant velocity V from the above equation can be derived to V =$\dfrac{v}{\sqrt{2}}$.
The general formula for the orbital velocity of a satellite orbiting around the earth is given by,
${{v}_{\circ }}=\sqrt{\dfrac{GM}{R+h}}....(1)$ where G is the gravitational constant, M is the mass of the earth R is the radius of the earth and h is the h is the height of the satellite from the surface. Initially the satellite was orbiting the earth with a orbital velocity of v but when the collision happened the meteorite and the satellite started moving with velocity $\dfrac{v}{\sqrt{2}}$, .i.e. the velocity decreased. If we compare equation 1 the velocity can only decrease if the height from the surface of the earth increases, cause all the remaining quantities are constants. This implies that the radius of orbiting the earth has increased.

So, the correct answer is “Option A”.

Note:
The above condition is a hypothetical condition. If all the above mentioned factors are taken care of then only the radius of orbiting will increase. We have also ignored the external force by the other planets to be also zero.