Question

A satellite of mass $1000\;kg$ is supposed to orbit earth at a height of $2000\;km$ above the Earth’s surface. Find its time period. Mass of the Earth = $6 \times 10^{24}\;kg$.

Answer 1

Remember that for a satellite to stay in orbit there should be a balance between the gravitational and the centrifugal forces that it is subjected to. Additionally, by assuming that the satellite orbit traces a circular perimeter and calculating the orbiting velocity of the satellite from the balance of the abovementioned forces you can find the time period.

Formula used:
Centrifugal force: $F_{centrifugal} = \dfrac{m\;v^2}{r}$, where m is satellite mass, v is its velocity and r is the radius of its orbit.
Gravitational force: $F_{gravitational} = \dfrac{G\;M\;m}{r^2}$ , where G is the gravitational constant, M is the mass of the body around which satellite is orbiting, m is the satellite mass and r is the distance to the satellite from orbiting centre.
In general, for a circular orbit, time period $T = \dfrac{Perimeter}{Velocity} = \dfrac{2 \pi r}{v}$

Complete step by step answer:

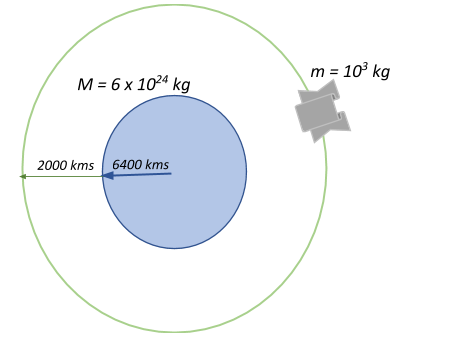
Let us look at the forces that are acting on a satellite orbiting the earth.
Firstly, there is the earth’s gravitational force that tugs on the satellite and pulls it closer:
$F_{gravitational} = \dfrac{G\;M\;m}{r^2}$
Secondly, due to the circular motion of the satellite it experiences a centrifugal force that pushes that satellite away:
$F_{centrifugal} = \dfrac{m\;v^2}{r}$
Now the satellite maintains its orbit by balancing the gravitational force and the centrifugal force. At equilibrium $F_{gravitational} = F_{centrifugal}$:
$\Rightarrow \dfrac{G\;M\;m}{r^{2}} = = \dfrac{m\;v^2}{r} \Rightarrow v = \sqrt{\dfrac{GM}{r}}$
Here, $G$ is the Gravitational constant ($6.67 \times 10^{-11}\;Nm^2kg^{-2}$), M is the mass of the earth and r is the radius of the satellite orbit given by:
$r = R + h = 6400 + 2000 = 8400kms$
Therefore, $v = \sqrt{\dfrac{GM}{r}} = \sqrt{\dfrac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{8400 \times 10^3}} \Rightarrow v = 6.9\;kms^{-1}$
Now, for a circular orbit, time period $T = \dfrac{Perimeter}{Velocity} = \dfrac{2 \pi r}{v}$
$\Rightarrow T = \dfrac{2 \pi (8400 \times 10^3)}{6.9 \times 10^3} =7649.095\;s = 2.12 hrs$
Therefore, the time period of revolution for the satellite is 2.12 hrs.

Note:
Always remember to include the Earth’s radius in addition to the distance of the satellite from the Earth’s surface while considering orbital radius as the magnitude of influence of Earth’s gravity depends on the distance of the satellite from the orbiting centre which is the centre of the Earth.
Proceed cautiously while converting km or $kms^{-1}$ to $m$ or $ms^{-1}$ and account for every power of 10.