Question

A satellite describes an elliptic orbit about a planet. Denoting by $r_0$ and $r_1$, the distances corresponding to the perigee and apogee of the orbit. The radius of curvature of the orbit at point A and B in terms of $r_0$ and $r_1$ is $\frac{\alpha r_0 r_1}{3(r_0+r_1)}$. The value of $\alpha$ is.

Answer 1

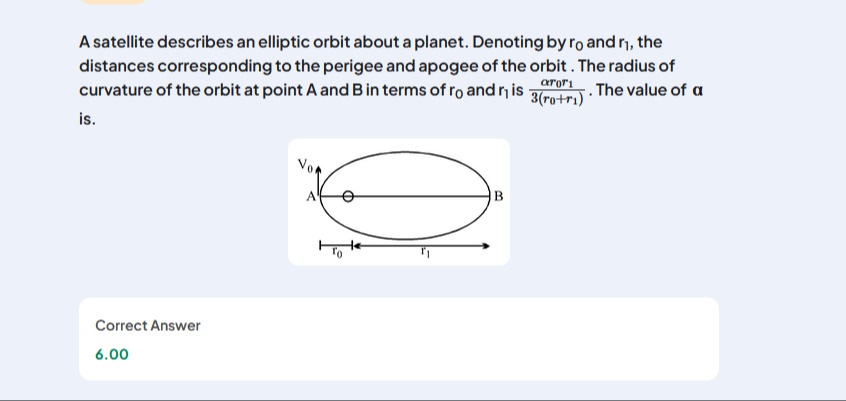
6.00

Answer 2

The radius of curvature of an ellipse at the vertices of the major axis (perigee and apogee in this case, as the planet is at a focus) is given by $\rho = \frac{b^2}{a}$, where $a$ is the semi-major axis and $b$ is the semi-minor axis of the ellipse.

Let $r_0$ be the distance at perigee (point A) and $r_1$ be the distance at apogee (point B).
For an elliptical orbit with the focus at the origin, the perigee distance is $r_0 = a(1-e)$ and the apogee distance is $r_1 = a(1+e)$, where $e$ is the eccentricity.

Adding these two equations gives $r_0 + r_1 = 2a$, so the semi-major axis is $a = \frac{r_0 + r_1}{2}$.
The distance from the center to the focus is $c = ae$. From $r_1 - r_0 = 2ae$, we get $e = \frac{r_1 - r_0}{2a} = \frac{r_1 - r_0}{r_0 + r_1}$.
The relationship between $a$, $b$, and $e$ is $b^2 = a^2(1-e^2)$.
$b^2 = a^2 (1-e)(1+e) = (a(1-e))(a(1+e)) = r_0 r_1$.
So, the square of the semi-minor axis is $b^2 = r_0 r_1$.

The radius of curvature at the perigee and apogee is $\rho = \frac{b^2}{a}$.
Substituting the expressions for $a$ and $b^2$ in terms of $r_0$ and $r_1$:
$\rho = \frac{r_0 r_1}{(r_0 + r_1)/2} = \frac{2r_0 r_1}{r_0 + r_1}$.

The question states that the radius of curvature of the orbit at point A and B is given by $\frac{\alpha r_0 r_1}{3(r_0+r_1)}$.
Comparing this with our derived expression:
$\frac{2r_0 r_1}{r_0 + r_1} = \frac{\alpha r_0 r_1}{3(r_0+r_1)}$.
Assuming $r_0 > 0$ and $r_1 > 0$, we can cancel $r_0 r_1$ and $r_0 + r_1$ from both sides (since $r_0+r_1 > 0$).
$2 = \frac{\alpha}{3}$.
Solving for $\alpha$:
$\alpha = 2 \times 3 = 6$.