Question

A saree 5.5 m long and 1.25 m wide has zari border 2.5 cm broad along its length on either side. Along the width on one edge the border was 5 cm wide and on the other side the zari was 25 cm wide. Find the area of the zari.

Answer 1

Hint: First find the area of zari along the length. Next, use the same method and find the area of zari along the breadth. Now add both the areas of zari then you will get the total area of zari border. This area is your required result.

Complete step-by-step answer:
Rectangle: In Euclidean plane geometry, a rectangle is quadrilateral with 4 right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal. It can also be defined as a parallelogram containing a right angle. It is a two-dimensional shape.
Beside above definition we can also define the rectangle as a combination of strips of breadth db upto b each of length l.

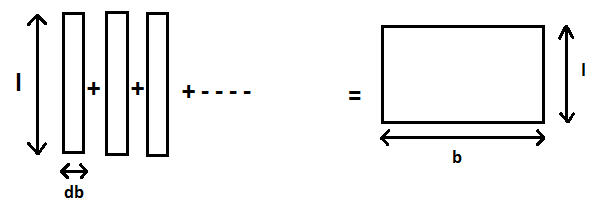
As you can see if we integrate the area of strip from $x = 0$ to $x = b$, we get the area of rectangle:
Area of rectangle $= \int\limits_0^b {ldb}$
As l does not depend on b we can bring it out.
Area of rectangle $= l\int\limits_0^b {1db}$
By basic principles of integration, we know the relation as:
$\int {1dx} = x + c$
By substituting this, we can write the equation as:
Area of rectangle $= l\left[ x \right]_0^b$
By substituting the limits into function, we get the equation:
Area of rectangle $= l\left( {b - 0} \right)$
By above proof we have the area of rectangle as:
Area of rectangle $= l \times b$
By given condition, we can write the positions of zari as:
5.5m long, 2.5cm broad along length, 5cm increase in breadth or 5cm decrease in length.
By using this we can draw the saree as:

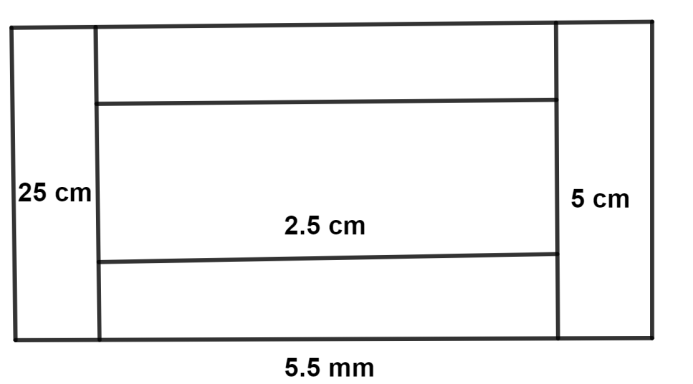
Area of border along the length can be calculated as
$2 \times$(Area of rectangle of length 5.5m and breadth 2.5cm)
We know that the area of the rectangle is $l \times b$, where l is the length and b is the breadth of the rectangle.
First converting 5.5m into cm. By relations we have relation:
$1m = 100cm$
By multiplying 5.5 on both sides we get it as:
$5.5m = 5.5 \times 100cm$
By simplifying the above equation we can write it as:
$5.5m = 550cm$
By substituting it into the above area equation, we get:
Area of border along length $= 2 \times \left( {550cm \times 2.5cm} \right)$
By simplifying, we get the area value as follows:
Area $= 2 \times 1375\,c{m^2}$
By simplifying, we get the area along length as follows:
Area of border along length $= 2750\,c{m^2}$ ……………….(1)
Area of border along breadth can be described as:
(Area of rectangle of length $\left( {25 + 5} \right)\,\,\,;\,\,\left( {125 - 5} \right)$breadth)
By substituting these into area formula, we can write it as:
Area of border $= \left( {\left( {25 + 5} \right)\,\left( {125 - 5} \right)} \right)$
By simplifying the above equation we can write it as:
Area of border $= \left( {30 \times 120} \right)$
By simplifying we get the area along breadth as follows:
Area of border along breadth $= 3600\,c{m^2}$ ……………….(2)
The total area of border can be written in form:
Total area of border $= \left( {Area\,\,along\,\,length + \,Area\,\,along\,\,breadth} \right)$
By substituting equation (1), (2) into this equation, we get:
Total area of border $= 2750\,c{m^2} + 3600\,c{m^2}$
By simplifying we get it as follows:
Total area of zari border $= 6350c{m^2}$
Therefore the total area of zari is $6350c{m^2}\,\,or\,\,0.635\,{m^2}$.

Note: Be careful while converting 5.5m into cm. Don’t forget while in length you must multiply 2 but in breadth you have different widths of 25.5. So, just add them and broadness is decreased by 5cm. Alternate method is from the diagram, you can see 2 rectangles. Find difference between areas of 2 rectangles. Anyways you get the same result.