Question

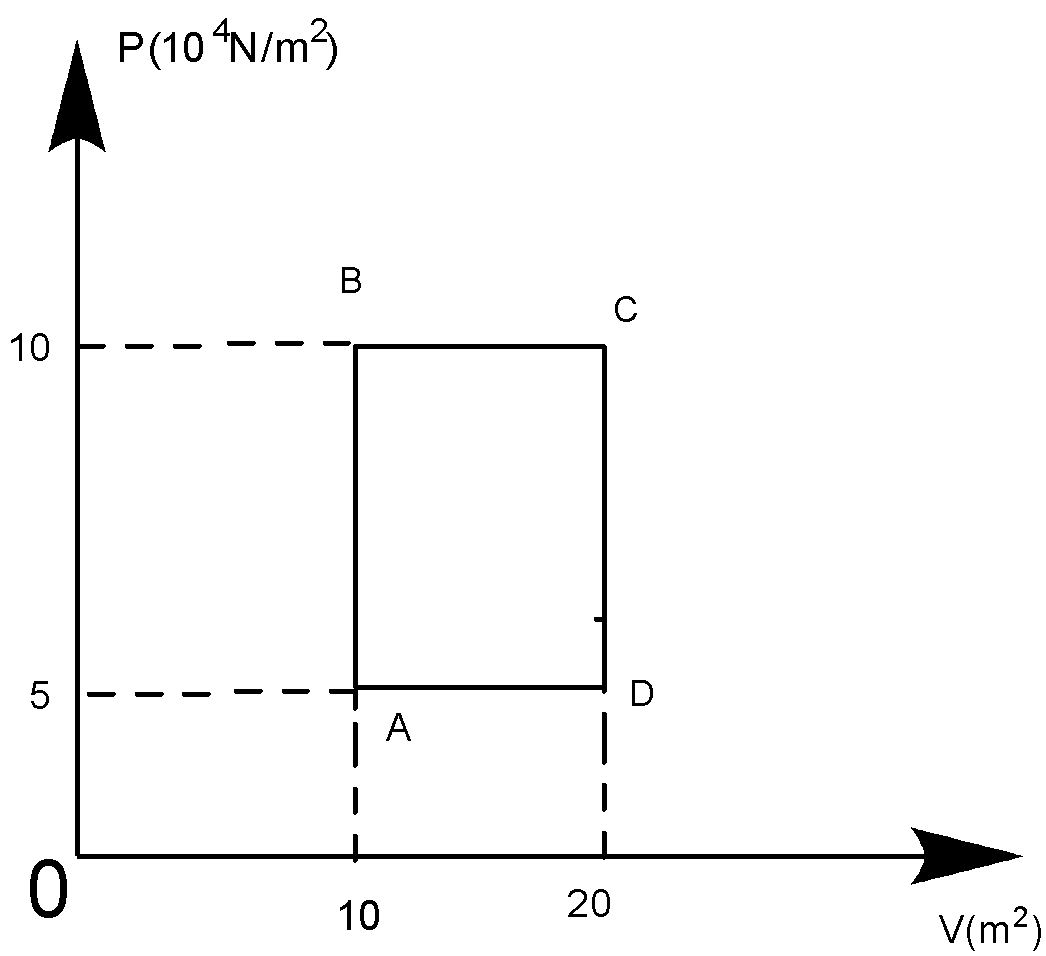
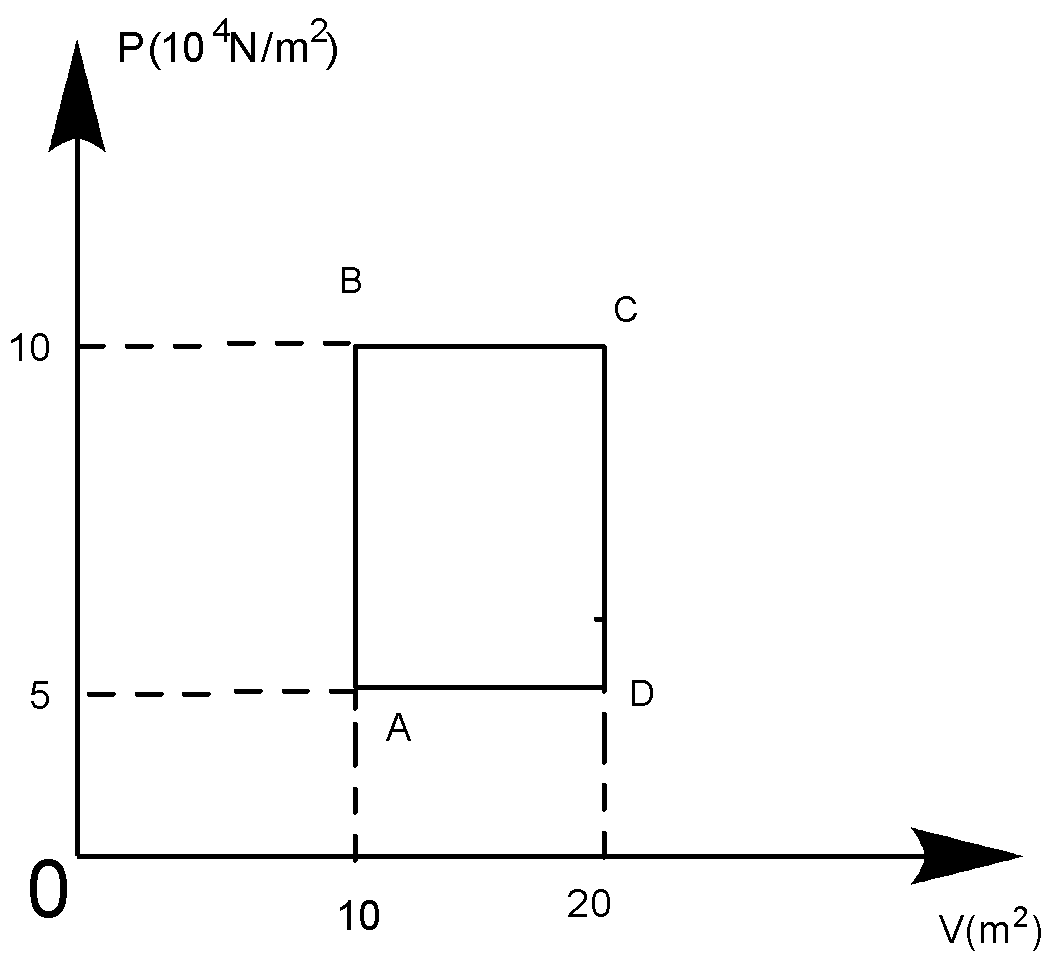
A sample of $2kg$ of helium (assumed ideal) is taken through the process $ABC$ and another sample of $2kg$ of the same gas is taken through the process$ADC$, then the temperature of the states $A$ and $B$ are:
[Given $R=8.3{joules}/{mol}\;K$]

$\left( A \right).\,\,{{T}_{A}}=120.5K,{{T}_{B}}=120.5K$
$\left( B \right).\,\,{{T}_{A}}=241K,{{T}_{B}}=241$
$\left( C \right).\,\,{{T}_{A}}=120.5K,{{T}_{B}}=241K$
$\left( D \right).\,\,{{T}_{A}}=241K,{{T}_{B}}=482K$

Answer 1

One mole of ideal gas has a capacity of $22.710$ litres at standard temperature and pressure (a temperature of $273.15K$ and an absolute pressure of exactly ${{10}^{5}}Pa$ ) as defined by IUPAC since $1982$.

Complete step by step answer:

$\left( a \right)n=\dfrac{2\times {{10}^{3}}}{4}=500=\dfrac{Given mass}{atomic mass}$
At A, ${{P}_{A}}{{V}_{A}}=nR{{T}_{A}}$
Or ${{T}_{A}}=\left( \dfrac{{{P}_{A}}{{V}_{A}}}{nR} \right)$
$\therefore {{T}_{A}}=\dfrac{\left( 5\times {{10}^{4}} \right)\times 10}{500\times 831}=120.33K$
At B, ${{P}_{B}}{{V}_{B}}=nR{{T}_{B}}$
${{T}_{B}}=\dfrac{{{P}_{B}}{{V}_{B}}}{nR}=\dfrac{\left( 10\times {{10}^{4}} \right)\times 10}{500\times 831}=240.66K$
So, $120.33K$ can be written approx $120.5K$. Whereas, $240.66K$ can be written approx. $241K$.
So, the answer becomes the $\left( C \right)$ option.

Additional Information:
Let us understand the ideal gas equation. This equation tells the effect of pressure and temperature on the volume of ideal gas.
It can be derived as following:
According to Boyle's law, the volume of gas is inversely proportional to pressure.
$\Rightarrow V\propto \dfrac{1}{P}$
According to charle’s law, the volume is directly proportional to temperature.
$\Rightarrow$ $V\propto T$
According to Avogadro’s law, the volume is directly proportional to no. of moles.
$\Rightarrow$ $V\propto n$
Combining all these equations we get.
$\Rightarrow$ $V\propto \dfrac{1}{P}\times T\times n$
$V=\dfrac{RTn}{P}\Rightarrow PV=nRT$
$R\to$ Gas constant
The ideal gas concept is useful because it obeys the ideal gas law and it is a simplified equation of state. The laws that deal with ideal gases are called ideal gas laws. The laws given by Boyle’s and Charle’s are ideal gas laws. The ideal gas equation holds well as long as it is under low density. Moreover, this equation is applicable for single gas or even for mixture of multiple gases. Ideal gas equation is also known as the general gas equation.

Note: Only ideal gas follows the ideal gas equation. Ideal gas is the one in which all collisions between atoms or molecules are perfectly elastic and in which there are no intermolecular attractive forces. Ideal gas also follows Raoult’s law. Real gases do not follow the ideal gas equation.