Question

A sample of 2kg Helium (assumed ideal) is taken through the process ABC and another sample of 2kg of the same gas is taken through the process ADC, then the temperature of the states A and B is:
Given: ${\text{R }} = 8.3{\text{joule/mol K}}$

A.${{\text{T}}_{\text{A}}}{\text{ = 120}}{\text{.5K, }}{{\text{T}}_{\text{B}}}{\text{ = 120}}{\text{.5K}}$
B.${{\text{T}}_{\text{A}}}{\text{ = 241K, }}{{\text{T}}_{\text{B}}}{\text{ = 241K}}$
C.${{\text{T}}_{\text{A}}}{\text{ = 120}}{\text{.5K, }}{{\text{T}}_{\text{B}}}{\text{ = 241K}}$
D.${{\text{T}}_{\text{A}}}{\text{ = 241K, }}{{\text{T}}_{\text{B}}}{\text{ = 120}}{\text{.5K}}$

Answer 1

Volume and pressure for both the samples of Helium can be calculated from the diagram. No. of moles can be calculated by dividing the mass in grams with the molar mass of helium and ${\text{R}}$ is a constant which will be the same in both the cases. Solve individual reactions separately to the value of temperature.
Formula used:
${\text{PV = nRT}}$
Where ${\text{P}}$ is pressure, ${\text{V}}$ is volume, ${\text{n}}$ is number of moles, ${\text{R}}$ is universal gas constant and ${\text{T}}$ is temperature.
Number of moles, ${\text{n = }}\dfrac{{{\text{mass of substance (in grams)}}}}{{{\text{molar mass of substance (in gmo}}{{\text{l}}^{{\text{ - 1}}}}{\text{)}}}}$

Complete step by step answer:
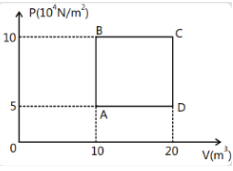
We need to calculate the value of temperature at stage A and B with the given parameters. On the $x$ axis of the graph volume in ${{\text{m}}^3}$ has been plotted and on $y$ axis pressure in ${\text{1}}{{\text{0}}^4}{\text{N/}}{{\text{m}}^2}$ has been plotted. What this means is we have to multiply the value we get on the $y$ axis with ${\text{1}}{{\text{0}}^4}$ to get the actual value of pressure.
So this is a ${\text{P - V}}$ curve. The coordinates of points will give us the value of volume and pressure.
Let us first do it for stage A. If we look at the diagram point A cuts $x$ axis at point 10 that means the volume of gas at point A will be ${{\text{V}}_{\text{A}}}{\text{ = 10 }}{{\text{m}}^{\text{3}}}$ and it cut $y$ axis at point 5, so the pressure at stage A will be ${{\text{P}}_{\text{A}}}{ = 5 \times 1}{{\text{0}}^{\text{4}}}{\text{ }}{{\text{m}}^{\text{3}}}$. Mass of helium is 2kg or 2000g and the molar mass of helium is ${\text{4 gmo}}{{\text{l}}^1}$.

{\text{ = 500 moles}} \\\\$$ Using the equation $${{\text{P}}_{\text{A}}}{{\text{V}}_{\text{A}}}{\text{ = }}{{\text{n}}_{\text{A}}}{\text{R}}{{\text{T}}_{\text{A}}}$$ and rearranging $${{\text{T}}_{\text{A}}}{\text{ = }}\dfrac{{{{\text{P}}_{\text{A}}}{{\text{V}}_{\text{A}}}}}{{{{\text{n}}_{\text{A}}}{\text{R}}}}$$ Now, substituting the values and solving we get, $${{\text{T}}_{\text{A}}}{\text{ = }}\dfrac{{{\text{5} \times 1}{{\text{0}}^{\text{4}}}{\text{} \times 10}}}{{{\text{500} \times 8}{\text{.3}}}} \\\ {\text{ = 120}}{\text{.5 K}} \\\\$$ So the temperature at stage A is $${\text{120}}{\text{.5 K}}$$. The mass of the gases is the same in both cases. The number of moles will be the same because molar mass is fixed. If we look at the diagram point B cuts $$x$$ axis at point 10 that means the volume of gas at point A will be $${{\text{V}}_{\text{A}}}{\text{ = 10 }}{{\text{m}}^{\text{3}}}$$ and it cuts $$y$$ axis at point 10. So, the pressure at stage A will be $${{\text{P}}_{\text{A}}}{\text{} = 10 \times 1}{{\text{0}}^{\text{4}}}{\text{ }}{{\text{m}}^{\text{3}}}$$. Using the same formula by replacing A with B we get, $${{\text{T}}_{\text{A}}}{\text{ = }}\dfrac{{{\text{10} \times 1}{{\text{0}}^{\text{4}}}{\text{} \times 10}}}{{{\text{500} \times 8}{\text{.3}}}} \\\ {\text{ = 240}}{\text{.9 K}} \\\\$$ Rounding off will give us the temperature 241K. **Hence, from the above calculations, option C is the correct option.** **Note:** The above graph is an example of Gay lussac’s law which state that pressure is directly proportional to temperature required volume and numbers of moles are constant. Since the gas is the same that is helium and if we carefully look at the graph, we will get to know that volume is the same for both the stage A and B. The number of moles is already the same as calculated by us. And we saw results, if we doubled the pressure from 5 to 10 then temperature also doubled. Hence, pressure and temperature is directly proportional to each other.