Question

A salt of ${M^ + }{X^ - }$ crystallizes with an FCC unit cell. If the edge length of the cell is 508 pm and the radius of the cation is 110 pm. What is the radius of the anion?

Answer 1

The ionic crystals consist of different sizes of cations and anions and packing of these ions into a crystal structure is much more complex than metallic crystal. In simple ionic compounds, anions are normally greater in size as compared to cations so are arranged in the closest-packed array while cations tend to occupy voids in the crystal structure.

Complete answer:
We know that in an FCC unit cell, atoms are present in the corners as well as each face centre of the cubic lattice. Some key points for the structure formed when ${M^ + }{X^ - }$ crystallizes in FCC lattice are as follows:
1. The anions i.e., ${X^ - }$ ions form FCC type of arrangement that means it contains ${X^ - }$ ions at the corners and at each face centre of the cubic lattice.
2. The cations i.e., ${M^ + }$ ions occupy all the octahedral sites of the cubic lattice.
3. Because there is only one octahedral site for every anion, so stoichiometry is $1:1$.
The structure formed will be as follows:

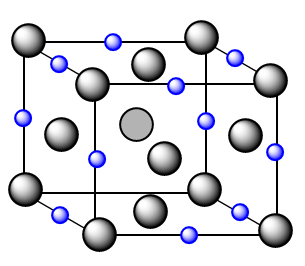
In the diagram, black sphere represents anions and blue spheres represent cations. Now, it is clearly observed from the diagram that one edge of the cubic lattice consists of two anions and one cation whose radius can be compared with the edge length to get the desired answer.
The edge of the cubic lattice can be represented as follows:

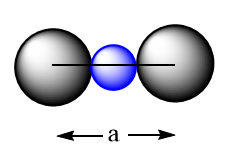
So, as per diagram the relation between edge length, radius of anion and radius of cation can be expressed as follows:
$a = {r_{{X^ - }}} + 2{r_{{M^ + }}} + {r_{{X^ - }}}$
On substituting values as per given in question, the radius of anion can be calculated as follows:
$a = 2\left( {{r_{{X^ - }}} + {r_{{M^ + }}}} \right)$
$\Rightarrow 508 = 2\left( {{r_{{X^ - }}} + 110} \right)$
$\Rightarrow {r_{{X^ - }}} = \dfrac{{508}}{2} - 110$
$\Rightarrow {r_{{X^ - }}} = 144pm$
Thus, we can conclude that the radius of anion for the given salt structure is 144 pm.

Note:
Sometimes students might get confused between FCC and CCP unit cells. Always remember that when in an FCC unit lattice, atoms are placed in octahedral voids, then the packing is formed of the type ABCABC which is also known as CCP lattice. So, the CCP is an alternative term of FCC unit lattice.