Question

A rubber ball is dropped from a height of 5m on a plane. On bouncing it rises to 1.8m. The ball loses its velocity on bouncing by a factor of
A. $\dfrac{16}{25}$
B. $\dfrac{2}{5}$
C. $\dfrac{3}{5}$
D. $\dfrac{9}{25}$

Answer 1

Firstly, you could recall Newton's equation of motion. Then, you could separately apply this for the motion of the ball when dropped and after bounce. Then, you could substitute these in the expression for finding the fractional change and thus find the answer to the given question.

Formula used:
Equation of motion, ${{v}^{2}}-{{u}^{2}}=2as$

Complete answer:
In the question, we are given a rubber ball that is dropped from a height of 5m on a plane. This ball rises to a height of 1.8m after bouncing. We are asked to find the loss of velocity on bouncing from the given information.
In order to solve the given question, we could use the equation of motion that is given by,
${{v}^{2}}-{{u}^{2}}=2as$ …………………………………………….. (1)

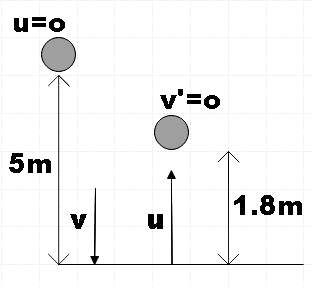
As the ball is being dropped, the initial velocity of the ball can be taken as zero and let the velocity with which the ball hits the floor 5m below be v then,
${{v}^{2}}-{{0}^{2}}=2g\times 5$
$\therefore v=\sqrt{10g}$ ………………………………….. (2)
Let the ball be bounced at u velocity and at maximum height (1.8m) the velocity will be zero,
${{0}^{2}}-{{u}^{2}}=-2g\times 1.8$
$\therefore u=\sqrt{3.6g}$ …………………………………… (3)
Then, we could find the loss of velocity by,
$\dfrac{v-u}{v}=\dfrac{\sqrt{10g}-\sqrt{3.6g}}{\sqrt{10g}}$
$\Rightarrow \dfrac{v-u}{v}=1-\sqrt{\dfrac{3.6g}{10g}}=1-\dfrac{6}{10}$
$\Rightarrow \dfrac{v-u}{v}=\dfrac{4}{10}$
$\therefore \dfrac{v-u}{v}=\dfrac{2}{5}$
Therefore, we found that the ball loses its velocity on bouncing by a factor of $\dfrac{2}{5}$.

Hence, option (B) is found to be the correct answer.

** Note:**
While solving the question we have assigned signs for acceleration due to gravity as per convention. That is, we have taken g as positive when the motion is downwards and g as negative for upward motion. Also, always remember the initial velocity when dropped and final velocity at maximum height is zero.