Question

A round table cover has six equal designs as shown in fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs. 3.5 per square cm. (Use $\sqrt{3}$ = 1.7)

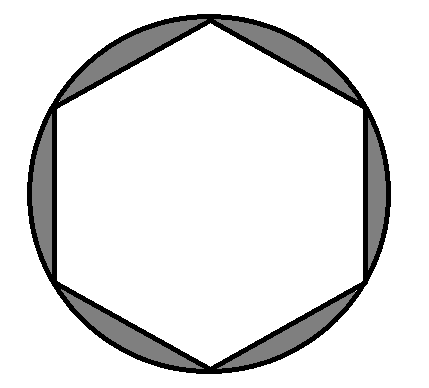
A. Rs. 1145.3
B. Rs. 1348
C. Rs. 1626.8
D. Rs. 1723.5

Answer 1

Hint:For solving this problem, first we divide the whole design into 6 sectors. Now we calculate the area of one sector and the area of the triangle associated with the sector. Now subtraction of both the areas will give us the desired area. Multiplying the resultant area by 6 will give us the whole area. Finally multiplying with the course will give us the total cost.

Complete step-by-step answer:
According to the problem statement, the radius of the circle is 28 cm. Since, it is a hexagon so the angle subtended will be, $\theta =\dfrac{{{360}^{\circ }}}{6}={{60}^{\circ }}$. The possible diagrammatic representation will be:

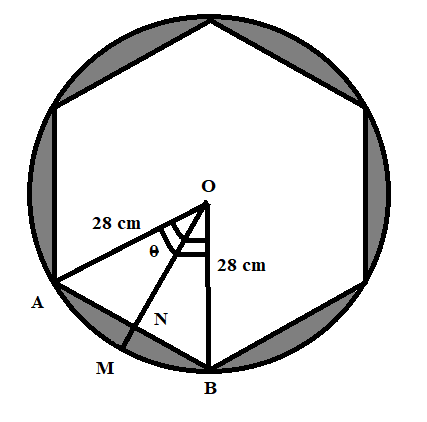
Now, we have to calculate the area of the sector OAMB,
Area of the OAMB$=\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}}=\dfrac{{{60}^{\circ }}}{{{360}^{\circ }}}\times \dfrac{22}{7}\times 28\times 28$
Area of the OAMB$=\dfrac{1232}{3}c{{m}^{2}}=410.67c{{m}^{2}}$
Now, we have to prove both the triangles $\Delta ONA$ and $\Delta ONB$ are congruent.
In $\Delta ONA$ and $\Delta ONB$
$\angle ONA=\angle ONB$ (both are 90 degree)
$OA=OB$ (Radii of the same circle)
$ON=ON$ (Common side )
$\therefore \Delta ONA\cong \Delta ONB$ by using RHS (right angle, hypotenuse and side) congruency.
By using properties of congruence, we get

& AN=NB=\dfrac{1}{2}\times AB \\\ & \angle AON=\angle BON=\dfrac{1}{2}\times \angle AOB=\dfrac{{{60}^{\circ }}}{2}={{30}^{\circ }} \\\ \end{aligned}$$ Applying $\text{cos3}{{\text{0}}^{\circ }}\text{ and }\sin {{30}^{\circ }}$ in the triangle ONA, we get $\begin{aligned} & \cos {{30}^{\circ }}=\dfrac{ON}{OA}=\dfrac{\sqrt{3}}{2}=\dfrac{ON}{28} \\\ & ON=14\sqrt{3}cm \\\ & \sin {{30}^{\circ }}=\dfrac{AN}{OA}=\dfrac{1}{2}=\dfrac{AN}{28} \\\ & \Rightarrow AN=14cm \\\ \end{aligned}$ The length of AB is twice the length of AN. So, $\begin{aligned} & 2AN=14\times 2=28cm \\\ & AB=28cm \\\ \end{aligned}$ Now, the area of triangle AOB, $\begin{aligned} & ar\Delta AOB=\dfrac{1}{2}\times AB\times ON=\dfrac{1}{2}\times 28\times 14\sqrt{3} \\\ & ar\Delta AOB=196\sqrt{3}c{{m}^{2}}=196\times 1.7c{{m}^{2}} \\\ & ar\Delta AOB=333.2c{{m}^{2}} \\\ \end{aligned}$ The area of one design =area of OAMB – area of $\Delta AOB$ The area of one design $$=\text{ }410.67c{{m}^{2}}-333.2c{{m}^{2}}~=77.47c{{m}^{2}}$$. The area of 6 designs $=6\times 77.47c{{m}^{2}}=464.82c{{m}^{2}}$. As per the given statement, cost of the $1c{{m}^{2}}=\text{Rs}\text{.3}\text{.5}$ Now, the cost of total area of design, i.e.$464.82c{{m}^{2}}=Rs.\left( 464.82\times 3.5 \right)$ Cost of $464.82c{{m}^{2}}=Rs.1626.8$. Hence, the cost of making the design at the rate of $$Rs.3.50c{{m}^{2}}\text{ is }Rs.1626.8$$ Therefore, option (c) is correct. Note: Students must be careful while proving the triangles congruent and should use the correct congruence rule to establish required relation. The angle subtended at the centre should be obtained with relation to the geometrical figure.Student should remember formula of area of triangle ,area of sector and trigonometric ratios for solving these types of problems.