Question
Question: A round ball of radius r subtends an angle \(\alpha \) at the eye of the observer, while the angle o...
A round ball of radius r subtends an angle α at the eye of the observer, while the angle of elevation of its center is β. Prove that the height of the center of the ball is r⋅sinβ⋅cosec2α.
Solution
Angle subtended at the eye of the observer will be the angle made by tangents touching the circumference circle and meeting the eye of the observer. An angle of elevation is the angle made by the line joining the eye and the center of the ball and the horizontal axis.
Draw the required figure.
First, find the value of side OC by using:
sinθ=HP in △OAC.
Height, of the center of the ball will be given by side OD, for calculating that apply:
sinθ=HP in △OCD, and put the value of OC found above.
Complete step by step answer:
Let O be the center of the given circle and eye of the observer be at C.
And AC, BC be the tangents to the circle at A and B respectively.
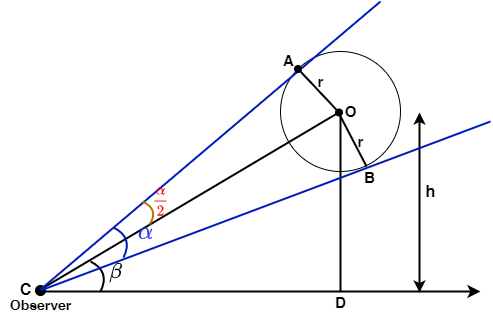
Let the height of the center of the ball be h.
⇒OD=h
Given,
The angle of elevation of the center is β
⇒∠OCD=β
The angle subtended at the eye of the observer is α
⇒∠ACB=α
To prove,
h=r⋅sinβ⋅cosec2α
Here, the triangles AOC and BOC are congruent by RHS congruence.
∴∠ACO=∠BCO=2α (by CPCT)
In △OAC:
sin2α=OCOA ⇒sin2α=OCr ⇒OC=sin2αr ⇒OC=r⋅cosec2α - - - - - - - - - - - - - - - (1)
Now, in △OCD:
sinβ=OCOD ⇒sinβ=OCh ⇒h=sinβ⋅OC ⇒h=sinβ⋅(r⋅cosec2α) ⇒h=r⋅sinβ⋅cosec2α
Hence, proved.
Note: The problems on this topic (Height and Distances) requires basic knowledge of trigonometry you should be aware of basic trigonometric ratios and their values.
In the given △MNO:
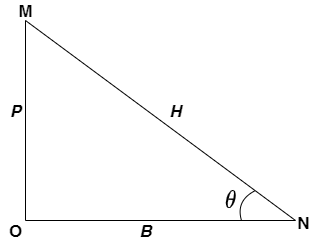
sinθ=HP=MNOM cosecθ = PH=OMMN cosθ=HB=MNON secθ = BH=ONMN tanθ=BP=ONOM cotθ = PB=OMON
