Question

A rope tied between two poles and a weight of 40N is suspended from its middle point. The rope sags by an angle of 1$^{\circ }$ , the tension in the rope will be-
(A) less than 40N
(B) Equal to 40N
(C) Greater than 40N
(D) None

Answer 1

In this case, after the weight is suspended from the middle, the object is in equilibrium state. The Lami’s theorem is applicable for a body in static equilibrium supported by 3 coplanar, concurrent and non-collinear forces. Applying the Lami’s theorem, we can solve for the tension of the rope.
Formula Used:
For three concurrent forces, the Lami’s theorem gives us,
$\dfrac{A}{\sin \alpha }=\dfrac{B}{\sin \beta }=\dfrac{C}{\sin \gamma }$
Where A, B and C are three vectors and $\alpha ,\beta ,\gamma$ are the angles made by the vectors.

Complete answer:
Lami's theorem states that for 3 forces acting at a point in equilibrium, each force is proportional to the sine of the angle between the other two forces. This theorem is applicable in this case because after suspending the weight the body is in equilibrium under the influence of the three forces.
The tension in the string is due to the weight of the body. Thus, we can attain the free body diagram for the problem as follow,

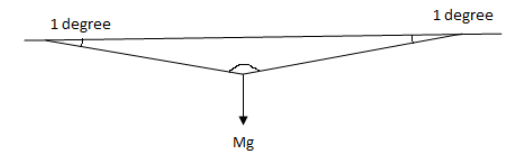
Fig: free body diagram for a suspended object
This free body diagram is equivalent to $\Rightarrow$

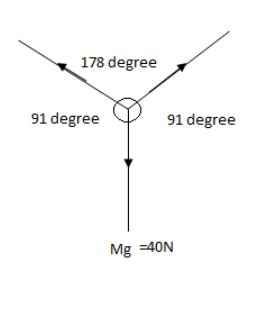
Applying the Lami’s theorem and plugging in the values of force and angle between the two forces, we have,

& \dfrac{Mg}{\sin ({{178}^{\circ }})}=\dfrac{T}{\sin ({{91}^{\circ }})} \\\ & \Rightarrow \dfrac{40N}{\sin ({{178}^{\circ }})}=\dfrac{T}{\sin ({{91}^{\circ }})} \\\ & \Rightarrow T=\dfrac{40\times \sin ({{91}^{\circ }})}{\sin ({{178}^{\circ }})} \\\ & \Rightarrow T=1145.97N \\\ \end{aligned}$$ Therefore, the tension in the string is much greater than 40N. **Thus the correct option is (C).** **Additional Information:** Lami’s theorem is applicable in static analysis of mechanical systems and structural systems. The theorem is named after Benard Lamy and uses the concepts of static equilibrium, parallelogram of force and vector addition. **Note:** While solving this problem, the first important step is to identify that the Lami’s theorem is applicable in this case. Then we need to calculate the angles that the forces make with each other. After making correct measurements of the angles between the forces, we need to plug in the values of the angles and the forces to obtain the value of the unknown tension.