Question

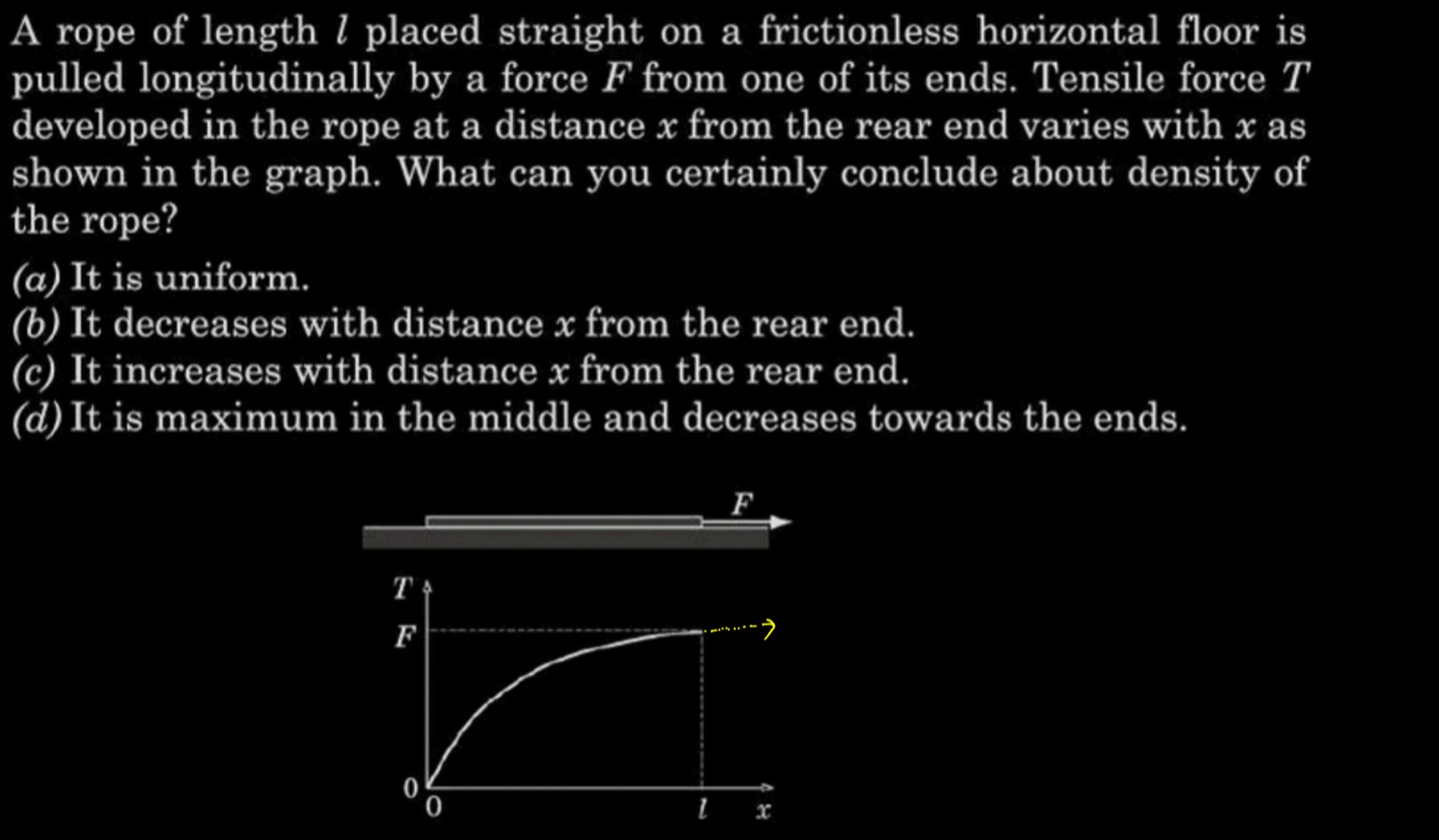
A rope of length $l$ placed straight on a frictionless horizontal floor is pulled longitudinally by a force $F$ from one of its ends. Tensile force $T$ developed in the rope at a distance $x$ from the rear end varies with $x$ as shown in the graph. What can you certainly conclude about density of the rope?

• A. It is uniform.
• B. It decreases with distance $x$ from the rear end.
• C. It increases with distance $x$ from the rear end.
• D. It is maximum in the middle and decreases towards the ends.

Answer 1

Answer: (B)

(b)

Answer 2

To determine the variation of the rope's density, we analyze the tensile force $T$ in the rope.

1. Define the system and variables:

   • Length of the rope: $l$
   • Applied force: $F$ at one end (let's assume the front end, $x=l$).
   • Distance $x$ is measured from the rear end ($x=0$).
   • Mass per unit length (linear density) of the rope: $\lambda(x)$.
   • The rope is on a frictionless horizontal floor.
   • Since the rope is pulled by a force $F$, it will accelerate. Let the acceleration of the entire rope be $a$. Since it's a rigid body (or in this context, an inextensible rope), all parts of the rope move with the same acceleration $a$.

2. Interpret the graph and tensile force:

   • The graph shows $T(0) = 0$ and $T(l) = F$.
   • $T(x)$ is the tensile force at a distance $x$ from the rear end. This force is responsible for accelerating the segment of the rope from $0$ to $x$.
   • Let $m(x)$ be the mass of the rope segment from $0$ to $x$.
   • $m(x) = \int_0^x \lambda(x') dx'$.

3. Apply Newton's Second Law:

   • The net force on the segment of the rope from $0$ to $x$ is $T(x)$.
   • According to Newton's second law, $T(x) = m(x) \cdot a$.
   • Substituting $m(x)$: $T(x) = a \int_0^x \lambda(x') dx'$

4. Relate tensile force to density:

   • To find $\lambda(x)$, we differentiate $T(x)$ with respect to $x$. Using the Fundamental Theorem of Calculus: $\frac{dT}{dx} = a \frac{d}{dx} \left(\int_0^x \lambda(x') dx'\right) = a \lambda(x)$
   • So, the slope of the $T$ vs $x$ graph, $\frac{dT}{dx}$, is directly proportional to the linear density $\lambda(x)$, with the constant of proportionality being the acceleration $a$.

5. Analyze the graph's slope:

   • Observe the shape of the given $T$ vs $x$ graph. The curve is concave down.
   • This means that the slope $\frac{dT}{dx}$ is decreasing as $x$ increases. Visually, the tangent to the curve is steepest near $x=0$ and becomes flatter as $x$ approaches $l$.

6. Conclude about density:

   • Since $\frac{dT}{dx} = a \lambda(x)$ and $a$ is a positive constant (the rope is accelerating), if $\frac{dT}{dx}$ decreases as $x$ increases, then $\lambda(x)$ must also decrease as $x$ increases.

Therefore, the density of the rope decreases with distance $x$ from the rear end.