Question

A rope is wound around a hollow mass of 3 kg and radius of 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
$\begin{aligned} & \text{A}\text{. 5m/}{{\text{s}}^{\text{2}}} \\\ & \text{B}\text{. 25m/}{{\text{s}}^{\text{2}}} \\\ & \text{C}\text{. 0}\text{.25rad/}{{\text{s}}^{\text{2}}} \\\ & \text{D}\text{. 25rad/}{{\text{s}}^{\text{2}}} \\\ \end{aligned}$

Answer 1

Hint: First find the torque applied on the cylinder using the formula $\tau =r\times F$, then find its moment of inertia using the formula $I=m{{r}^{2}}$. Finally find the angular acceleration of the cylinder using the formula $\tau =I\alpha$.

Formula used:
$\tau =r\times F$
$I=m{{r}^{2}}$
$\tau =I\alpha$

Complete step by step answer:
Given,
Mass of the hollow cylinder m = 3 kg
Radius of the cylinder r = 40 cm = 0.4 m
The force with which the rope is pulled = 30 N

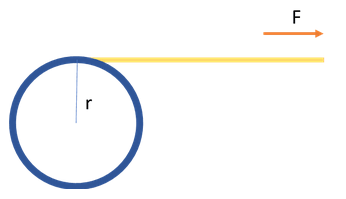
Since the rope is wound around the cylinder, pulling it, the rope will impart a torque on the cylinder and set it in motion. The torque acted upon is given by,
$\tau =r\times F$
Assuming the rope is pulled tangentially and the rope doesn’t slip, the torque will be,
$\tau =0.4m\times 30N=12Nm$
I is the moment of inertia of the hollow cylinder is given by,
$I=m{{r}^{2}}$
Substituting the values, we get
$I=3\times {{(0.4)}^{2}}=0.48kg{{m}^{2}}$
As a result of the torque, there will be an angular acceleration α, where α and τ is related by,
$\tau =I\alpha$

Finally, the angular acceleration will be,
$\begin{aligned} & \alpha =\dfrac{\tau }{I} \\\ & \Rightarrow \alpha =\dfrac{12}{0.48}=25\text{rad/}{{\text{s}}^{\text{2}}} \\\ \end{aligned}$
So, the angular acceleration of the cylinder if the rope is pulled with a force of 30 N is $25\text{rad/}{{\text{s}}^{\text{2}}}$.
Therefore, the correct option is D.

Note: It is assumed that the rope is pulled without slipping (in which case the effective torque would be less). As a result of this angular acceleration, the cylinder will start moving in the direction of the force.