Question

A rope is used to lower vertically a block of mass m at a distance x at a constant downward acceleration$\dfrac{g}{2}$. The work done by the rope on the block is:

& A)mgx \\\ & B)\dfrac{1}{2}mg{{x}^{2}} \\\ & C)-\dfrac{1}{2}mgx \\\ & D)mg{{x}^{2}} \\\ \end{aligned}$$

Answer 1

Here , Concept of Newton’s Second law of motion is applied because different forces are acting on the body and acceleration is also acting then from here we get the value of force which is responsible for work done and then we apply the formula for work along with the direction of force and displacement.

Complete step-by-step solution:
Since it is given in the question that rope is used to hang a block of mass m. So tension in the block is acting in upward direction because weight of block is acting in downward direction.
Let us assume the tension of the block is T acting in upward direction.
Weight mg of the block is acting in downward direction and body is going downward by distance x through a constant acceleration of $\dfrac{g}{2}$ .
So the body shifted downward by distance x.
See in the figure ,

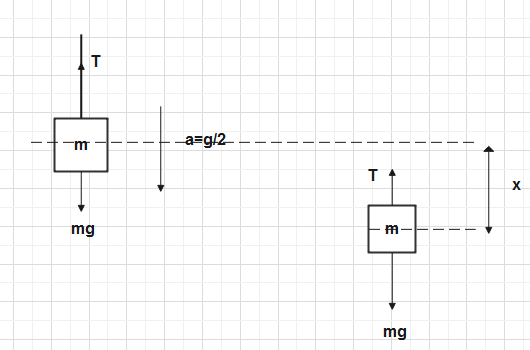
Since , weight mg is acting in downward direction and Tension T is acting in upward direction and acceleration is also acting in downward direction. So according to Newton’s Second Law of Motion. We can write the equation as :-
$mg-T={{F}_{net}}$- - - - - - - Equation 1
since net force is equal to the product of mass and acceleration.
${{F}_{net}}=ma$- - - - - - - - - Equation 2
from Equation1 and 2
\Rightarrow $$$$mg-T={{F}_{net}}
\Rightarrow $$$$mg-T=ma
\Rightarrow $$$$T=mg-ma
Since acceleration is given in the question as $a=\dfrac{g}{2}$.Put this value in above equation we get,
\Rightarrow $$$$T=mg-m\dfrac{g}{2}
\therefore $$$$T=m\dfrac{g}{2}.
Since work is equal to the dot product of force and displacement.
$Work=\overrightarrow{F}.\overrightarrow{d}$
$\Rightarrow W=FdCos\theta$
Here calculation of work force is equal to tension because we have to find work on the block by rope.
Put the value of Force as Tension T and displacement as x. In the given figure Tension T and displacement x are in opposite direction so angle between is taken as ${{180}^{0}}$.So work done becomes,
$W=TxCos{{180}^{0}}$
\Rightarrow $$$$W=-m\dfrac{g}{2}x
$\therefore W=-\dfrac{1}{2}mgx$
This is the required expression for work done by rope on the block.
So Correct Option is C.

Note: Whenever we have to calculate the work done for anybody then we always have to consider the angle between the direction of force and displacement in the formula of work no matter either work itself is a scalar quantity .So Work done is always defined as a scalar product of force and displacement .