Question

A roller coaster is designed such that riders experience “weightlessness” as they go around the top of a hill whose radius of curvature is $20m$. The speed of the car at the top of the hill is between
(A) $14m/s$and $15m/s$
(B) $15m/s$and $16m/s$
(C) $16m/s$and $17m/s$
(D) $13m/s$and $14m/s$

Answer 1

Hint
When a body performs circular motion, a force which is always towards the center of the circle acts on the body. By balancing the acting forces at the top of the hill and using Newton's laws of motion we can find the speed of the ride.
$\Rightarrow F = \dfrac{{m{v^2}}}{R}$

Complete step by step answer
First let us draw the forces acting on the ride,

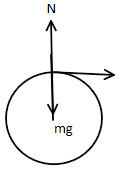
When the ride reaches the topmost point of the circle, then the force acting on the ride is shown in the figure. You can see that the weight ‘mg’ acts downwards (here m is the mass and g is the acceleration due to gravity), its counterpart normal force ‘N’ will act upwards, velocity ‘v’ will be tangential to the curve. Due to circular motion centripetal force will act on the body. There is no acceleration seen in the vertical direction.
On balancing forces,
$\Rightarrow mg - N = \dfrac{{m{v^2}}}{r}$, where r is the radius of curvature and v is the velocity
The term weightlessness is given which means N=0
So, $mg = \dfrac{{m{v^2}}}{r} \Rightarrow v = \sqrt {rg}$
Substituting the values, $r = 20m,g = 10m/{s^2}$
$\Rightarrow v = \sqrt {20 \times 10} = 14.12m/{s^2}$
Hence the speed of car at the top will be between $14m/s$and $15m/s$
Correct option is (A); $14m/s$and $15m/s$.

Additional Information
Centripetal force is a center directed force without which circular motion is not possible. It is not a new force, it can be frictional force, electrical force or any other.

Note
When a body is in circular motion on a path of ‘r’ radius with uniform velocity ‘v’, then it has centripetal acceleration which is constant in magnitude but continuously changing direction. This always acts towards the center of the circle.