Question

A rod whose length is $l$ bent at an angle $120^\circ$, Then find the centre of mass of bent shape.

Answer 1

In this question, use the concept of the resolving the components along the horizontal and the vertical direction with respect to the mass, length and the bend angle, then use the formula of the centre of mass coordinate along the horizontal and the vertical direction.

Complete step by step solution:
To find the centre of mass of the given rod, first we have to calculate the $x$ and the $y$coordinates of the centre of mass, that is
$\Rightarrow {x_{cm}} = \dfrac{{{m_1} \times {x_1} + {m_2} \times {x_2}}}{{{m_1} + {m_2}}}$
$\Rightarrow {y_{cm}} = \dfrac{{{m_1} \times {y_1} + {m_1} \times {y_2}}}{{{m_1} + {m_2}}}$
Where, ${x_{cm}}$ is centre of mass coordinate of the $x$axis, ${y_{cm}}$ is coordinate of centre of mass of the $y$axis, ${m_1} \times {x_1},{m_2} \times {x_2},{m_1} \times {y_1},{m_2} \times {y_2}$ are the products of smaller mass parts of the rod in both coordinates and to find the centre of mass coordinate, divide the sum of products with sum of all small mass parts.

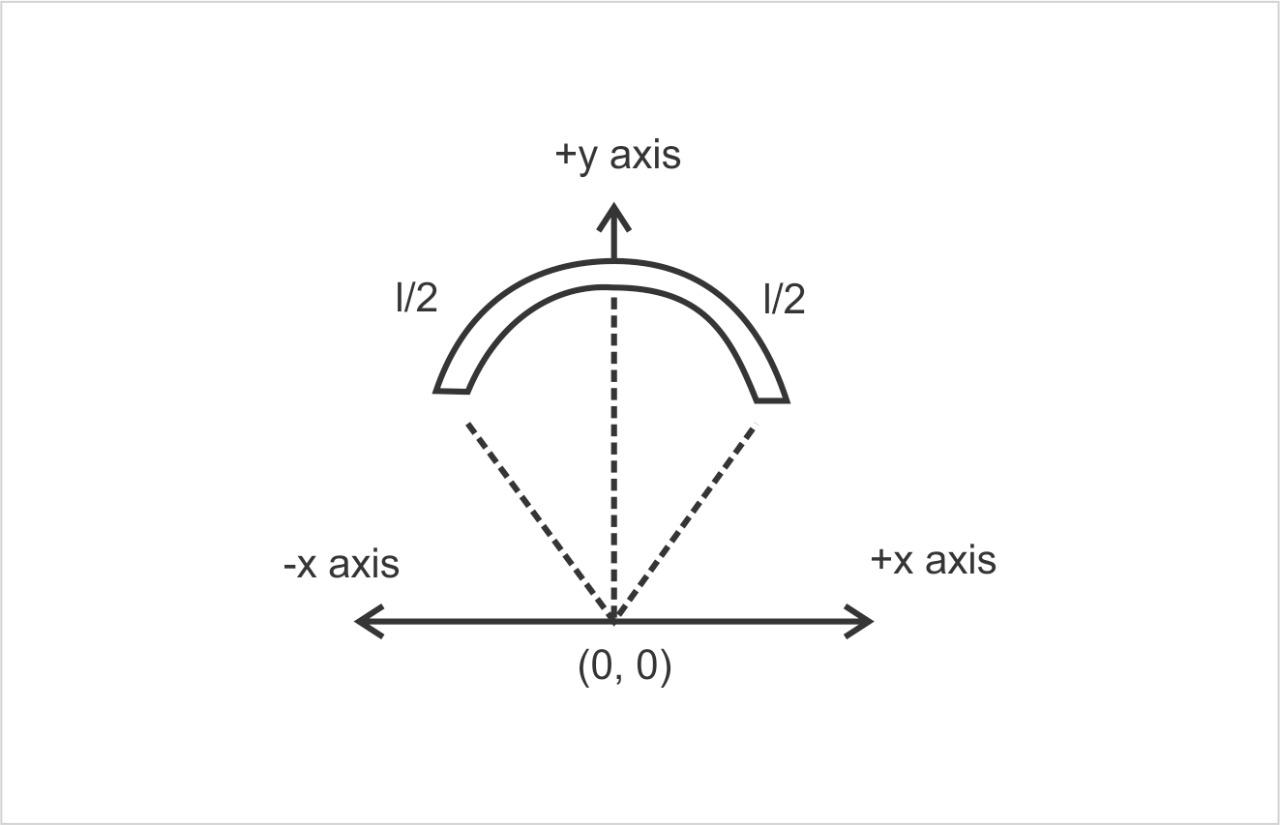
Diagram of calculating centre of mass
When the rod is bend in equally two parts, each part will have length $\dfrac{l}{2}$and its centre of mass will be in $\dfrac{l}{4}$ and mass will also be distributed equally, that is, $\dfrac{m}{2}$.
Now, as $\dfrac{l}{2}$ is in the negative $x$axis, sign of $\dfrac{l}{4}({x_1})$ will be negative in that axis, and ${x_2}$ will be $- \dfrac{l}{4}\cos \theta$ as the component in the $x$axis. In case of $y$axis, there is no value, so here $\dfrac{l}{4}({y_1})$ will be $0$, and the ${y_2}$will be $\dfrac{l}{4}\sin \theta$ as the positive component of $y$axis. Putting all the values in the centre of mass coordinate equations we get
$\Rightarrow {x_{cm}} = \dfrac{{ - \dfrac{m}{2} \times \dfrac{l}{4} - \dfrac{m}{2} \times \dfrac{l}{4}\cos \theta }}{{\dfrac{m}{2} + \dfrac{m}{2}}}$
On solving the above expression, we get
$\Rightarrow {x_{cm}} = - \dfrac{1}{2}\left( {\dfrac{l}{4} + \dfrac{l}{4}\cos \theta } \right)$
For $y$ axis centroid we get,
$\Rightarrow {y_{cm}} = \dfrac{{\dfrac{m}{2} \times 0 + \dfrac{m}{2} \times \dfrac{l}{4}\sin \theta }}{{\dfrac{m}{2} + \dfrac{m}{2}}}$
On solving the above expression, we get
$\Rightarrow {y_{cm}} = \dfrac{1}{2}\left( {\dfrac{l}{4}\sin \theta } \right)$
Let us assume that the distance of centre of mass be $k$it is expressed as
$\Rightarrow k = \sqrt {{x_{cm}}^2 + {y_{cm}}^2}$
Now, putting the values in the expression we get
$\Rightarrow k = \sqrt {{{\left( { - \dfrac{1}{2}\left( {\dfrac{l}{4}\cos \theta } \right)} \right)}^2} + {{\left( {\dfrac{1}{2} \times \dfrac{l}{4}\sin \theta } \right)}^2}}$
So, we get
$\Rightarrow k = \dfrac{l}{4}\cos \dfrac{\theta }{2}$
Now putting $\theta = 120^\circ$ we get the position of the centre of mass as,
$\Rightarrow k = \dfrac{l}{4}\cos \dfrac{{120^\circ }}{2}$
$\Rightarrow k = \dfrac{l}{4} \times \dfrac{1}{2}$
On simplification we get,
$\therefore k = \dfrac{l}{8}$

Note: In this question, In the calculation of the centre of mass, the mass gets omitted from both numerator and denominator, and the distance of centre of mass has trigonometric calculation to come to the result of the expression of $\cos \dfrac{\theta }{2}$.