Solveeit Logo
Login

Question

Question: A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizo...

A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is
A. W(d−x)x\dfrac{{W\left( {d - x} \right)}}{x}
B. W(d−x)d\dfrac{{W\left( {d - x} \right)}}{d}
C. Wxd\dfrac{{Wx}}{d}
D. Wdx\dfrac{{Wd}}{x}

Explanation

Solution

Hint In the question, the weight of the rod is supported by two parallel edges, it is in a horizontal position. Imaginate the situation by the given parameters and equation the forces of the positions, then we get the normal reaction on A.

Complete step by step answer
The situation is given below in the diagrammatic representation.

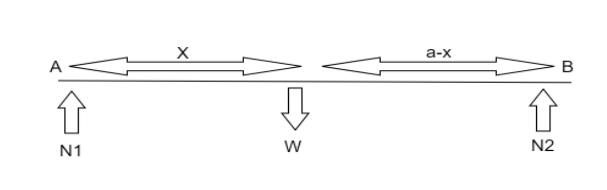
Where,
N1{N_1} be the Normal reaction on A,N2{N_2}be the Normal reaction on B and WWbe the weight of the rod.
Equating the forces and taking the vertical equilibrium by the normal reaction, we get
N1+N2=W........(1){N_1} + {N_2} = W........\left( 1 \right)
In the diagram, Torque balance about centre of mass of the rod, so we get the expression as
Nx=N2(d−x)........(2)Nx = {N_2}\left( {d - x} \right)........\left( 2 \right)
Convert the equation 1 in terms of the normal reaction on B, we get
N2=W−N1{N_2} = W - {N_1}
Substitute the value of N2{N_2}in the equation 2, we get
Nx=(W−N1)(d−x)Nx = \left( {W - {N_1}} \right)\left( {d - x} \right)
Simplify the above equation, we get
Nx=(Wd−Wx−N1d+Nx)Nx = \left( {Wd - Wx - {N_1}d + Nx} \right)
Taking the common terms and simplify the equation, we get
Nd=W(d−x)Nd = W\left( {d - x} \right)
Convert the equation in terms in terms of the normal reaction on A, we get
N1=W(d−x)d{N_1} = \dfrac{{W\left( {d - x} \right)}}{d}
Therefore, the normal reaction on A is W(d−x)d\dfrac{{W\left( {d - x} \right)}}{d}.

Hence from the above options, option B is correct.

Note In the question, we know that the two edges are in the same direction that is in the vertical position. So, vertical position, we will take it as positive. If it is in a horizontal position, we will take it as a negative sign. By equating the equations, the normal reaction on A has been calculated.