Question

A rod of uniform cross-sectional area A and length L has a weight W. It is suspended vertically from a fixed support. If the material of the rod is homogeneous and its modulus of elasticity is, I then determine the total elongation produced in the rod due to its own weight.

Answer 1

Start by writing the formula for elastic modulus. Find out the elongation for a small element of the road (dx). Integrate on the whole length of the rod to find out the required elongation of the entire rod.

Formula used:
Young’s modulus for elongation of a rod of length l when a force F (external) is acting on it is given as:
$Y = \dfrac{F/A}{\Delta l/l}$.

Complete step-by-step answer:
We no that modulus of elasticity is given as the ratio of stress acting (linearly) on the rod and the strain which produces elongation in the rod;
$Y = \dfrac{stress}{strain}$

Stress is nothing but the force per unit area acting on the body and strain is the ratio of change created in the length upon original length, so;
$Y = \dfrac{F/A}{\Delta l/l}$;

Here, A will be the area of the cross section of the rod and $\Delta l$ will be the elongation i.e., the difference of final length and initial length l.
The elongation can be written as: $\Delta l = \dfrac{l(F/A)}{I}$ ; where we replaced Y with I (given).
For an elongation of any smaller section dx of the rod we can write: $d(\Delta l) = \dfrac{F}{AI} dx$ ; here, we just used dx in place of l.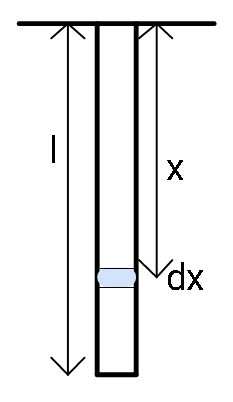
The force acting on this small element dx will be due to the rod weight below it.
Therefore, $F = \dfrac{W}{l} (l-x)$ ;
where, W/l is for uniform distribution of weight. Total elongation for the entire rod can be written as:
$\Delta l = \dfrac{W}{lAI} \int_{0}^{l} (l-x) dx = \dfrac{W}{lAI} \left(lx - \dfrac{x^2}{2} \right) \Bigg|_{0}^{l}$ .
This must give us the required total elongation as: $\Delta l = \dfrac{Wl}{2AI}$

Note: The integration was performed from zero to length l, by considering zero as the point where the rod is attached (or hanged). The distance x of the element dx was also measured from the point where the road was attached.