Solveeit Logo
Login

Question

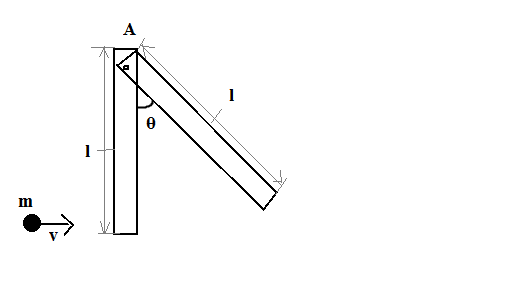
Question: A rod of mass \(m\) is hinged at upper end A as shown in the figure. A point object mass \(m\) strik...

A rod of mass mm is hinged at upper end A as shown in the figure. A point object mass mm strike at the lower end and stops. The maximum angle through which the rod will rotate (Givenv2<2gl3{v^2} < \dfrac{{2gl}}{3})

A) cos⁡−1(1−3v22gl){\cos ^{ - 1}}(1 - \dfrac{{3{v^2}}}{{2gl}})
B) cos⁡−1(1−3v2gl){\cos ^{ - 1}}(1 - \dfrac{{3{v^2}}}{{gl}})
C) cos⁡−1(1−v22gl){\cos ^{ - 1}}(1 - \dfrac{{{v^2}}}{{2gl}})
D) cos⁡−1(1−v2gl){\cos ^{ - 1}}(1 - \dfrac{{{v^2}}}{{gl}})

Explanation

Solution

Conservation of momentum, general law of physics in which there are no changes in an isolated object collection in the quantity called momentum, which characterises motion; namely the overall momentum of a system remains constant. Mullion is equal to the mass of an object multiplied by its speed and corresponds to the force needed in order to stop the object in a unit duration

Complete step by step solution:
The conservation of momentum and the conservation of energy and mass is a central principle of physics. Momentum is known as an object's mass multiplied by the object's speed. Momentum preservation indicates that the amount of momentum remains constant in some problem field; momentum is not created nor destroyed, but only changed through forces, as defined by Newton's laws of movement. It is harder to deal with momentum than mass and energy, as momentum is both a large and a directional vector quantity. In all three physical directions the momentum is maintained simultaneously. When dealing with gases, it is still more difficult because forces in one direction can influence momentum in another because of the collisions between many molecules. We will present a very, very simplified flow issue on this slide, where properties shift only in one direction.
Momentum conservation,
mv=mv1mv = m {v_1}
Where mm is the mass and v,v1v, {v_1} is the velocity
v1=v{v_1} = v
mgh=12mv12mgh = \dfrac{1}{2}m{v_1}^2
Where hh is the height
mgh=12mv2mgh = \dfrac{1}{2}m{v^2}
h=l2−l2cos⁡θh = \dfrac{l}{2} - \dfrac{l}{2}\cos \theta
mgl2(1−cos⁡θ)=mv22mg\dfrac {l} {2} (1 - \cos \theta) = \dfrac{{m{v^2}}}{2}
θ=cos⁡−1(1−v2gl)\theta = {\cos ^ {- 1}} (1 - \dfrac{{{v^2}}}{{gl}})

Note: The conservation of angular momentum is also fully determined by experimentation and can show mathematically that space is uniform in orientation, which means that there is nothing in the laws of nature which defines one direction of space as peculiar to any other.