Solveeit Logo
Login

Question

Question: A rod of mass m and length l is made to stand at an angle of \({60^0}\) with the vertical. Potential...

A rod of mass m and length l is made to stand at an angle of 600{60^0} with the vertical. Potential energy of the rod at this point is
A. mglmgl
B. mgl2\dfrac{{mgl}}{2}
C. mgl3\dfrac{{mgl}}{3}
D. mgl4\dfrac{{mgl}}{4}

Explanation

Solution

Since in the question no specific point has been stated, we shall calculate the potential energy of the center of mass of the rod. The center of mass is a point where the mass of the system can be considered to be concentrated. For a rod, it lies in the middle of the rod. The rod makes an angle of 600{60^0} with the vertical. So, we shall calculate the height of the center of mass above the reference line and substitute in the formula of potential energy given as U=mghU = mgh .

Complete answer:
Let us visualize the situation first.

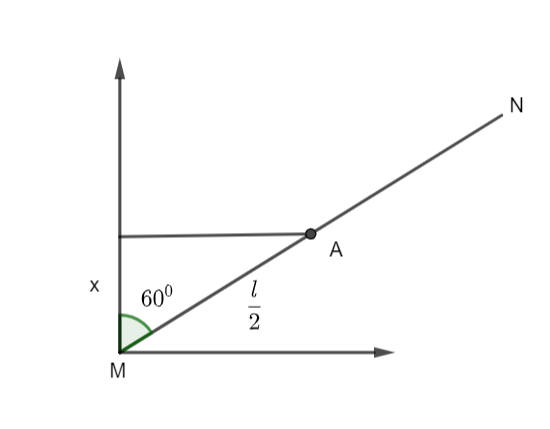
Here MN is the rod of length l making an angle of 600{60^0} with the vertical. A denotes the center of mass of the rod. Now, since the center of mass of a rod lies in the middle of the rod, MA=l2MA = \dfrac{l}{2} .
The potential energy of a point at a height h is given as U=mghU = mgh where m is the mass of the object and g is the acceleration due to gravity.
Since in the question no specific point has been stated, we shall calculate the potential energy of the center of mass of the rod.
The center of mass is a point where the mass of the system can be considered to be concentrated.
The mass will be equal to the mass of the rod.
So, for the point A, mass will be m.
The height will be given by x=l2cos⁡600x = \dfrac{l}{2}\cos {60^0}
⇒x=l4\Rightarrow x = \dfrac{l}{4}
Substituting in the formula of potential energy, we get,
U=mgxU = mgx
∴U=mgl4\therefore U = \dfrac{{mgl}}{4}
Hence, option D is the correct answer.

Note:
A center of mass is that point where the whole mass of the system can be considered to be concentrated. All the weighted position vectors relative to this point sum up to zero. A center of mass is just like another point in the object. It also experiences the same force and undergoes the same acceleration (except for rigid bodies). The gradient of potential energy gives the force experienced by the center of mass.