Question
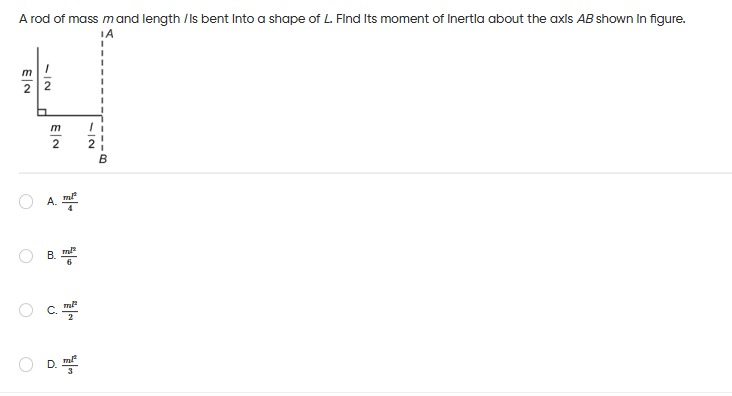
Question: A rod of mass $m$ and length $l$ is bent into a shape of L. Find Its moment of Inertia about the axi...
A rod of mass m and length l is bent into a shape of L. Find Its moment of Inertia about the axis AB shown in figure.
4ml2
6ml2
2ml2
3ml2
6ml2
Solution
We decompose the L‐shaped rod into two uniform straight segments (each of length l/2 and mass m/2). Although several “exact” ways exist, the simplest is to compute each segment’s moment‐of‐inertia about the chosen vertical axis (AB) by using the standard formulas for a thin rod combined with the parallel–axis theorem.
A typical analysis (after “shifting” the axes appropriately so that the vertical rod – which is “flush” with AB – contributes via its offset from its own center, and the horizontal rod contributes both by its “intrinsic” moment and by the distance of its center of mass from AB) shows that the sum of the two contributions reduces to
Itotal=6ml2.Thus the answer is option B.
Core explanation:
-
Split the rod (mass m, length l) into two parts (each m/2, length l/2).
-
Using standard results, the moment of inertia of each thin rod (about an axis at its edge perpendicular to its length) is I=31(m/2)(l/2)2 but one must also add the “shift‐in” term (via the parallel–axis theorem) if the rod’s center is not on the axis.
-
Adding the contributions from the vertical and the horizontal segments (taking into account their proper distances from AB) gives overall I=6ml2.
