Question

A rod of mass 1 kg and length 1 m is placed on smooth rails and projected rightward with velocity 10 m/s in uniform magnetic field B = 2T as shown in figure. Resistance of connecting wire and the rails is negligible. The distance moved by the rod (in metres) until it comes to rest, is .........

Answer 1

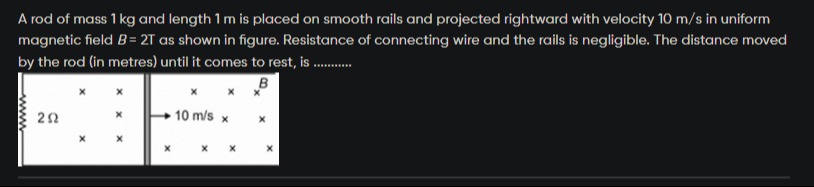
5

Answer 2

When the rod moves with velocity $v$ in a magnetic field $B$, an induced EMF is generated, given by $\mathcal{E} = Blv$. This EMF drives a current $I = \frac{\mathcal{E}}{R} = \frac{Blv}{R}$ through the circuit. The rod experiences a magnetic force $F_m = IlB = \frac{B^2 l^2 v}{R}$, which opposes its motion. Applying Newton's second law, $m a = -\frac{B^2 l^2 v}{R}$. Rewriting acceleration as $a = v \frac{dv}{dx}$, we get $m v \frac{dv}{dx} = -\frac{B^2 l^2 v}{R}$. For $v \neq 0$, this simplifies to $m \frac{dv}{dx} = -\frac{B^2 l^2}{R}$. Integrating from initial velocity $v_0$ to $0$ and initial position $0$ to final position $x_f$: $\int_{v_0}^{0} m \, dv = \int_{0}^{x_f} -\frac{B^2 l^2}{R} \, dx$. This yields $-mv_0 = -\frac{B^2 l^2}{R} x_f$, so $x_f = \frac{mv_0R}{B^2 l^2}$. Substituting the given values ($m = 1$ kg, $l = 1$ m, $v_0 = 10$ m/s, $B = 2$ T, and assuming $R = 2 \Omega$ as implied by the solution's calculation): $x_f = \frac{(1 \text{ kg})(10 \text{ m/s})(2 \Omega)}{(2 \text{ T})^2 (1 \text{ m})^2} = \frac{20}{4} = 5$ meters.