Question

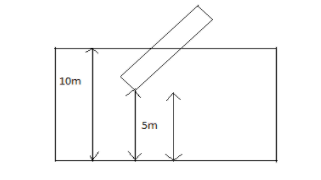
A rod of length ${\text{6m}}$ has specific gravity $\rho \left( { = 25/36} \right)$ . One end of the rod is tied to a ${\text{5m}}$ long rope, which in turn is tied to the floor of a pool ${\text{10m}}$ deep, as shown. Find the length $\left( {{\text{in}}\,\,{\text{m}}} \right)$ of the rod which is out of water.

Answer 1

Buoyant force or upthrust is an upward force exerted by a fluid that opposes the weight of a particular or fully immersed object. The center of buoyancy of an object is the centroid of the displaced volume of fluid.

Complete Step by step solution:
Given that, there is a rod having a length of 6m which is having a specific gravity of $\rho \left( { = 25/36} \right)$ and one end of the rod is tied to a ${\text{5m}}$ long rope and the rope is tied to the floor of a poll which is ${\text{10m}}$ deep. We have to find the length of the rod which is out of the water.
As we know for floating conditions the weight which is acting vertically downward must be equal to force of upthrust.
${F_b}$ is a center of buoyancy force acting on the middle of the rod.
$mg$ is a force acting at $1g$ at $l/2$ of the rod

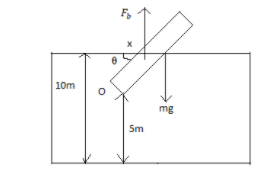
With the help of the above figure let’s try to solve the problem.
Now, let’s see how to calculate buoyant force on the rod:
${F_b}$ is the weight of the water displaced
$= \rho {A_c}(5/\sin \theta )g$
And on solving it we get
$\Rightarrow mg = \rho {A_c} \times 6g$
As, now according to the rotational equilibrium the net moment at point O must be zero for that rotation along clockwise must be equal to rotation along anti clock direction.
Total clockwise moment= total anticlockwise moment
Total clockwise moment
$\Rightarrow mg \times 3\cos \theta = \rho {A_c} \times 6g \times 3\cos \theta$ , and we will name it equation $1$
Total anti- clockwise moment $= {\rho _w}{A_c}(5/\sin \theta )g \times OA\cos \theta$
$mg = {\rho _w}{A_c}(5/\sin \theta )g \times (5/2\sin \theta )\cos \theta$ , and we will name it equation $2$
Now, by equation ${\text{1}}\,\,{\text{and}}\,\,{\text{2}}$ , we get
$\Rightarrow {\rho _w}{A_c}(5/\sin \theta )g \times (5/2\sin \theta )\cos \theta = \rho {A_c} \times 6g \times 3\cos \theta$
And on solving it further we get
$\Rightarrow {\sin ^2}\theta = (25/36) \times ({\rho _w}/\rho )$
And the value for the theta will be equal to,
$\Rightarrow \theta = {90^ \circ }$

Therefore, the length of the rod outside the water is ${\text{1m}}$ .

Note: Remember this process along with Archimedes principle and its application like buoyancy force (upthrust) formula which will make it easier to solve problems like these in future.