Question

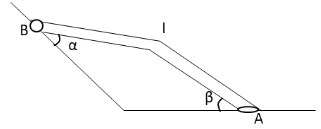
A rod of length ‘’ slides down along the inclined wall as shown in figure. At the instant shown in figure the speed of end A is ‘$v$’, then the speed of B will be:

A. $\dfrac{{v\sin \alpha }}{{\sin \beta }}$
B. $\dfrac{{v\sin \beta }}{{\sin \alpha }}$
C. $\dfrac{{v\cos \alpha }}{{\cos \beta }}$
D. $\dfrac{{v\cos \beta }}{{\cos \alpha }}$

Answer 1

Use the expression for law of conservation of linear momentum. This formula gives the relation between initial velocity of the object and final velocity of the object. Apply this law of conservation of linear momentum to the two ends A and B of the rod in the vertical direction and determine the value of speed of end B of rod.

Formula used:
The law of conservation of linear momentum states that
${P_i} = {P_f}$ …… (1)
Here, ${P_i}$ is the initial linear momentum of the object and ${P_f}$ is the final linear momentum of the object.

Complete step by step answer:
We have given that the length of the rod sliding along an incline wall is $l$. The angle made by end A of the rod with the inclined wall is $\beta$ and the angle made by the end B of the rod with the inclined wall is $\alpha$. The speed of end A of the rod is v. We have asked to determine the speed of end B of the rod. Let v’ is the speed of the end B of the rod and $m$ is the mass of the rod.

The centre of mass of the rod is acting in a downward direction on the rod. Hence, there is no torque acting on the rod. The velocity of the end A acting in the downward direction is
${v_A} = \dfrac{l}{2}v\sin \beta$
The velocity of the end B acting in the downward direction is
${v_B} = \dfrac{l}{2}v'\sin \alpha$

Apply law of conservation of linear momentum to the two ends A and B of the rod.
$m{v_A} = m{v_B}$
$\Rightarrow {v_A} = {v_B}$
Substitute $\dfrac{l}{2}v\sin \beta$ for ${v_A}$ and $\dfrac{l}{2}v'\sin \alpha$ for ${v_B}$ in the above equation.
$\Rightarrow \dfrac{l}{2}v\sin \beta = \dfrac{l}{2}v'\sin \alpha$
$\Rightarrow v\sin \beta = v'\sin \alpha$

Rearrange the above equation for $v'$.
$\therefore v' = \dfrac{{v\sin \beta }}{{\sin \alpha }}$
Therefore, the speed of end B of the rod is $\dfrac{{v\sin \beta }}{{\sin \alpha }}$.

Hence, the correct option is B.

Note: The students should keep in mind that we have used only vertical components of velocities of the ends A and B of the rod. So, the students should not forget to use only vertical components of speeds of ends A and B of the rod while determining the linear momentum of the ends of the rod.