Question
Question: A rod of length \[L\] with square cross-section \[\left( a\times a \right)\] is bent to form a circu...
A rod of length L with square cross-section (a×a) is bent to form a circular ring. Then the value of stress developed at points E and F respectively, (Y is Young's modulus of metal rod)
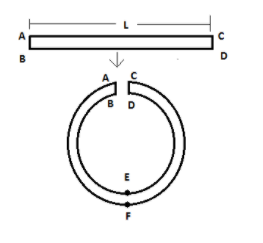
Solution
Here the length of dimensions of the rod and values of Young’s modulus are given. Question is to find the stress developed in the points E and F when the rod is bent to form a circular ring. To find the stress we can use the bending equation, which relates, young’s modulus, radius of curvature, distance of the layer at which the bending stress is considered.
Formula used:
circumference of circle = 2 !!π!! R
yσ=RE
Complete answer:
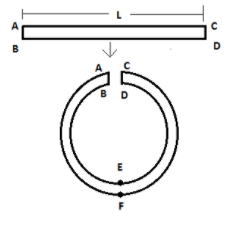
We have,
yσ=RE
Where,
σis the bending stress
Eis young’s modulus
y is the distance of the layer at which the bending stress is considered
R = Radius of curvature
Given, the length of wire is L. Let Rbe the radius of the circle. Then,
Circumference of the circle, 2πR=L
Then,
R=2πL
Given, Young’s modulus of metal rod is Y. i.e.,
E=Y
Given that, the rod has a square cross-section (a×a). Then,
y=2a
Then,
σ=REy=2πLY2a=L2πY2a=LπYa
Hence, then the value of stress developed at points E and F is LπYa.
Here, the point E experiences compression and point F experiences tension.
Therefore, answer is option C.
Note:
At the neutral axis of a beam, the bending stress is zero, which is coincident with the centroid of the beam's cross section. The bending stress increases as we move away from the neutral axis, and reaches the maximum value at the extreme fibers at the top and bottom of the beam.
