Question

A rod of length $l$ is standing vertically on a frictionless surface. It is slightly disturbed by its position. Let $\omega$ and $\alpha$ be the angular speed and angular acceleration of the rod, when the rod turns through an angle $\theta$ with the vertical, then find the value of the acceleration of the center of mass of the rod.

Answer 1

You can start by calculating the $\tau$ using the equation $\tau = mg\dfrac{l}{{2}}\sin \theta$. We know that the moment of inertia of a rod around its end is $M\dfrac{{L^2}}{{3}}$. Then compare the values of $\tau$ and $I$ by substituting these values in the equation $\tau = I\alpha$. Now you will obtain the value of $\alpha$. Then use the equation ${a_{CM}} = \alpha R$ to reach the solution.

Complete step by step answer:
In this problem, we are given a rod of length $l$, that is standing on a vertical frictionless surface. When it is slightly disturbed from this position. When it is disturbed, the force of gravity pulls it down and it causes an acceleration of the rod.

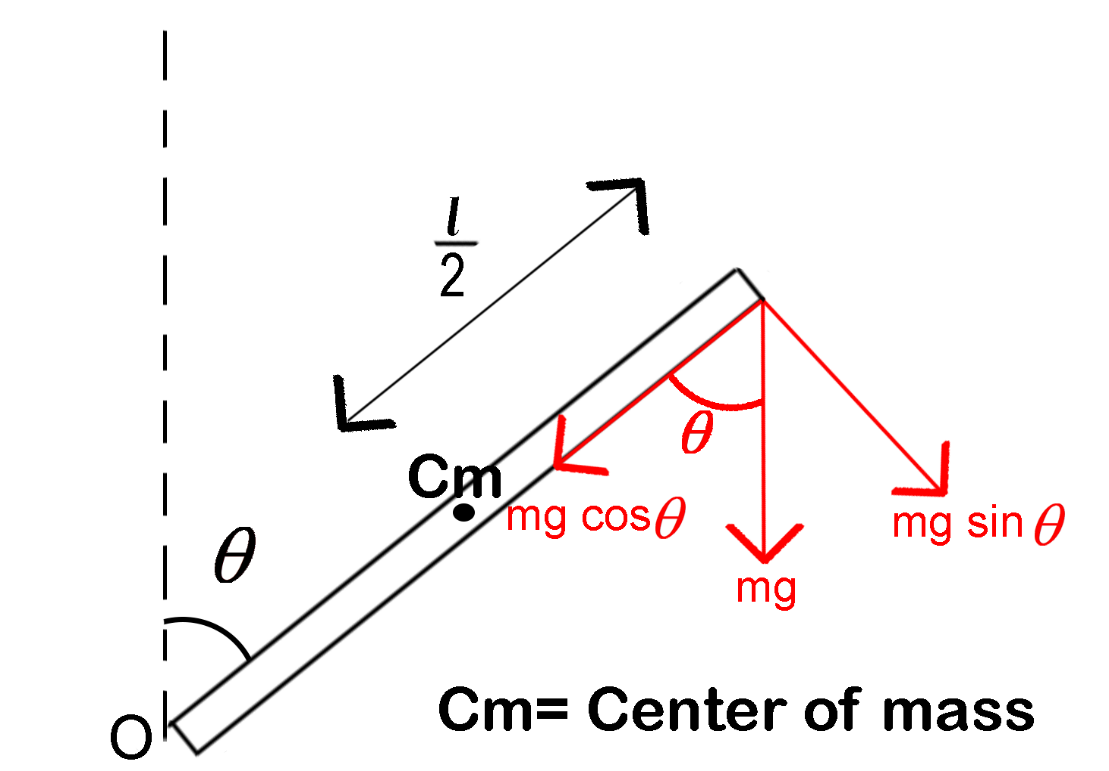
Let’s take the mass of the body be $m$.
Suppose that after a certain time the rod makes an angle $\theta$ with the vertical.
So, the torque of the rod at this point is
$\tau = mg\dfrac{l}{{2}}\sin \theta$ (Equation 1)
Here, we considered only half the length of the rod because the center of mass of a rod is located at a distance $\dfrac{l}{{2}}$ from either end.
We also know that moment of inertia of a rod about one of its end is
$I = M\dfrac{{L^2}}{{3}} = m\dfrac{{l^2}}{{3}}$ (Equation 2)
We know that for a rotating body
$\tau = I\alpha$
Here, $\tau =$ Torque
$I =$ Moment of inertia
$\alpha =$ Angular acceleration
Substituting the value of $\tau$ and $I$ from equation 1 and equation 2 respectively
$\tau = mg\dfrac{l}{{2}}\sin \theta$ = $m\dfrac{{l^2}}{{3}} \alpha$
$\Rightarrow \alpha = 3g \dfrac {sin \theta }{{2l}}$
We also know that
${a_{CM}} = R\alpha$
Here, ${a_{CM}} =$ acceleration of the center of mass
$R = \dfrac{{l}}{2}$
So,
${a_{CM}} = 3g \dfrac {sin \theta }{{2l}} \times \dfrac{l}{2}$
$\Rightarrow {a_{CM}} = 3g \dfrac {sin \theta }{{4}}m/{s^2}$
Hence, the acceleration of the center of mass is $3g \dfrac {sin \theta }{{4}}m/{s^2}$ .

Note:
In the solution above we used a concept called the concept of center of mass. The Center of the mass of a body is an imaginary point where all the mass of a body can be considered to be considered. In some cases, the center of mass of a body can be situated outside the body, for example – Center of mass of a Banana, safety pin, etc.