Question

A rod of length $L$ is pivoted at one end and is rotated with a uniform angular velocity in the horizontal plane. Let ${T_1}$ and ${T_2}$ be the tensions at the points. $\dfrac{L}{4}$ and $\dfrac{{3L}}{4}$ away from the pivoted ends then:
(A) ${T_1} > {T_2}$
(B) ${T_2} > {T_1}$
(C) ${T_1} = {T_2}$
(D) The relation between ${T_1}$ and ${T_2}$ whether the rod rotates clockwise or anticlockwise.

Answer 1

Hint : Here, we have to use the concept of rotational motion. As we have been given the rod of some length and asked to tie its one end to the fixed point and observe the tensions acting at some distances away from pivoted ends. Here, tension is equal to the centrifugal force acting on the end of the body which is rotating.

Complete Step By Step Answer:
We have the rod of length $L$ and one end is pivoted such that it rotates with uniform angular velocity $\omega$ in the horizontal plane. As shown in the figure below

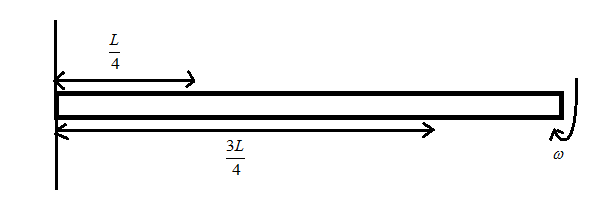
Let us first consider the part of length of $\dfrac{L}{4}$ consider the figure below:

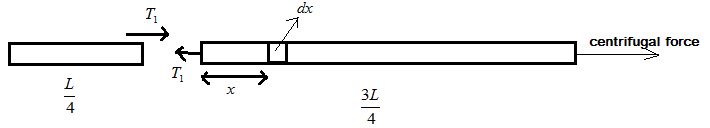
Here, we have resolved all the forces that are responsible for the tension in the rod, also let $M$ be the mass of rod
Thus, mass per unit length, $m = \dfrac{M}{L}$
Now tension acting on length $\dfrac{{3L}}{4}$ by $\dfrac{L}{4}$ is ${T_1}$ and it is equivalent to the centrifugal force acting at the end of length $\dfrac{{3L}}{4}$ .
Therefore,
${T_1}$ = the centrifugal force acting on the end of length $\dfrac{{3L}}{4}$
${T_1} = m{\omega ^2}x$
$x$ is the distance of center of mass
Now, we know that the $dx$ is the distance for which we have to calculate the centrifugal force,
Such that, $mdx$ be the mass at $dx$ varying in the limit between $x = \dfrac{L}{4}$ to $x = L$
${T_1} = \int\limits_{\dfrac{L}{4}}^L {mdx \times {\omega ^2} \times x}$
$\Rightarrow {T_1} = m{\omega ^2}\int\limits_{\dfrac{L}{4}}^L {xdx}$
$\Rightarrow {T_1} = m{\omega ^2}\left[ {\dfrac{{{L^2}}}{2} - \dfrac{{{L^2}}}{{32}}} \right]$ ….. (on putting all the limits)
$\boxed{ \Rightarrow {T_1} = m{\omega ^2}\dfrac{{15{L^2}}}{{32}}}$
Similarly, for ${T_2}$
We have to find tension ${T_2}$ acting by length $\dfrac{{3L}}{4}$ on length $\dfrac{L}{4}$ , consider the figure below:

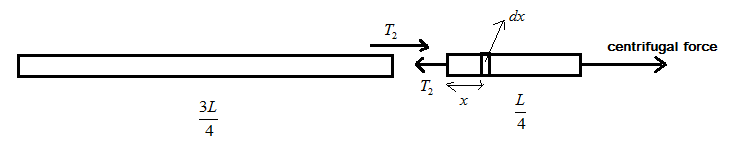
Follow the same procedure with limits $x = \dfrac{{3L}}{4}$ to $x = L$
${T_2} = m{\omega ^2}x$
$\Rightarrow {T_2} = \int\limits_{\dfrac{{3L}}{4}}^L {mdx \times {\omega ^2} \times x}$
$\Rightarrow {T_2} = m{\omega ^2}\left[ {\dfrac{{{L^2}}}{2} - \dfrac{{9{L^2}}}{{32}}} \right]$
$\boxed{ \Rightarrow {T_2} = m{\omega ^2}\dfrac{{7{L^2}}}{{32}}}$
Thus, from above conclusions we get that the tensions ${T_1} > {T_2}$
The correct answer is option A.

Note :
In these types of problems it is important to resolve the forces acting on each other partly or wholly because in the question the tension is asked at different lengths. We carried out the expressions by equating the forces and observed the answer and found out the comparison between tensions. This question can also be solved with the help of the concept of MOI of the rod. You can try yourself.