Question

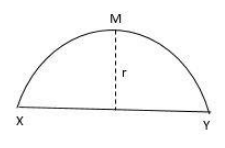
A rod of length L and mass M is bent to form a semi-circular ring as shown in figure. The moment of inertia about XY is:

A. $\dfrac{{M{L^2}}}{{2{\pi ^2}}}$
B. $\dfrac{{M{L^2}}}{{{\pi ^2}}}$
C. $\dfrac{{M{L^2}}}{{4{\pi ^2}}}$
D. $\dfrac{{2M{L^2}}}{{{\pi ^2}}}$

Answer 1

Moment of inertia of a rigid body about an axis of rotation is defined as the sum of product of the mass of each particle and the square of its perpendicular distance from the axis of rotation.
Formula used:
Moment of Inertia, $I = M{R^2}$
Here,M= mass of the ring
R=Perpendicular distance from the axis of rotation

Complete step by step answer:
Since, the rod is bent to form a semicircle, the line passing through the ends of the wire is equal to the diameter of the circle.
Let $r$ be the radius of the semi-circle.
The mass M of the rod can be assumed to be accumulated at the center of the rod.
Thus, the perpendicular distance between the center of mass, M and the axis of rotation will be $r.$

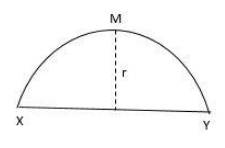
In this question, we have to find the moment of inertia along the XY axis. So the axis of rotation will be XY.
So, from the formula of moment of inertial and the explanation we gave above, we can write,
${I_{XY}} = M{r^2}$ . . . (1)
Where, ${I_{XY}}$is the moment of inertia along the XY axis.
Now, we know that the circumference of a circle is $2\pi r$
Therefore, the circumference of a semicircle is $\dfrac{{2\pi r}}{2} = \pi r$
Since, the length of the rod is L. We can say that
$L = \pi r$
Rearranging the above equation, we can write
$r = \dfrac{L}{\pi }$
Substituting this value in equation (1), we get
${I_{XY}} = M{\left( {\dfrac{L}{\pi }} \right)^2}$
$\Rightarrow {I_{XY}} = \dfrac{{M{L^2}}}{{{\pi ^2}}}$
Hence, the correct answer is (B) $\dfrac{{M{L^2}}}{{{\pi ^2}}}$

Note: Sometimes students have misconception about $R$, they take $R$ as the radius of the ring so always keep remember that $R$ is the perpendicular distance from the axis of rotation.