Question

A rod of length $\dfrac{f}{2}$​ is placed along the axis of a concave mirror of focal length $'f'$.If the near end of the real image formed by the mirror just touches the far end of the rod, find its magnification.

Answer 1

A concave mirror is a mirror whose reflecting surface is curved inwards which means that it faces towards the centre of the sphere. A concave mirror is also known as a converging mirror as it converges the rays of light towards the focus on passing through it.

Complete step by step answer:
The ray diagram of this question will be,

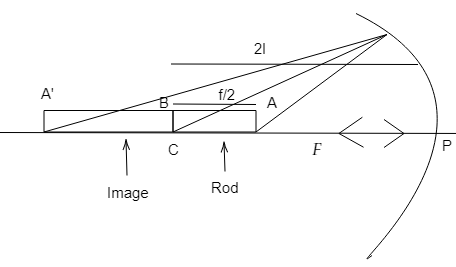
In this question, the near end of the real image of the rod is the image of far end $B$ of the rod $AB$. Now, this is possible only if the far end $B$ of the rod is placed at the centre of curvature $C$ of the concave mirror.
Let the image of near end $A$ of the rod be $A'$
We know that the radius of curvature $R$ can be written as $2f$ because the radius of curvature is twice the focal length.
Also, the object distance for near point of the rod A is $u$
$u = 2f - \dfrac{f}{2}$
$u = \dfrac{{3f}}{2}$
According to mirror formula,
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
This can also be written as,
$\dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u}.......(1)$
Here,
$u = - \dfrac{{3f}}{2}$ (negative sign is because the object is on the left side of the mirror)
$f = - f$ (as the focal length of a concave mirror is negative)
$v = ?$
On putting the given values in equation (1)
$\dfrac{1}{v} = \dfrac{1}{{ - f}} - \dfrac{1}{{\left( {\dfrac{{ - 3f}}{2}} \right)}}$
$\dfrac{1}{v} = \dfrac{1}{{ - f}} + \dfrac{2}{{3f}}$
On further solving the above equation, we get,
$\dfrac{1}{v} = \dfrac{{ - 3 + 2}}{{3f}}$
$\dfrac{1}{v} = \dfrac{{ - 1}}{{3f}}$
On taking the reciprocal on both the sides,
$v = - 3f$
The negative sign in the image distance indicates that the image $A'$ is formed on the same side of the object $A$.
The formula for magnification is $m = -\dfrac{v}{u}$
Here, $v = - 3f$ and $u = \dfrac{{ - 3f}}{2}$
On putting the values of $u$ and $v$,
$m = -\dfrac{{ - 3f}}{{\left( {\dfrac{{ - 3f}}{2}} \right)}}$
On further solving, we get,
$m = -2$
So, the value of magnification is $-2$.

Note:
Magnification is the increase in the image size produced by spherical mirrors with respect to the object size. The expression for magnification can be described in terms of both the height of the object and the image as well as the distance of the object and the image from the poles.