Question
Question: A rod of length 50 cm is pivoted at one end. It is raised such that if made an angle of \({{30}^{{}^...
A rod of length 50 cm is pivoted at one end. It is raised such that if made an angle of 30∘ from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in rad s−1) will be(g=10ms−2)
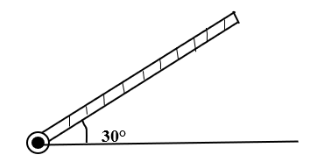
A. 30B. 230C. 230D. 220
Solution
Hint: It is based on conservation of energy - energy can neither be created nor be destroyed but can be transferred from one form to another form or one body to another body.
Total energy is the sum of kinetic energy and potential energy, where the total energy of a system is constant, so whenever kinetic energy increases potential energy decreases and vice versa to make total energy constant.
Here, when the rod is kept at 30° to horizontal due to its position it contains potential energy and when it is released from rest this stored potential energy is converted into kinetic energy making the total energy constant.
Complete step by step answer:
Let us consider a rod of length 50 cm as shown below:
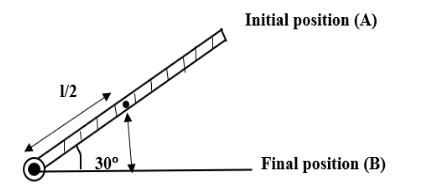
When the rod is raised to a point then its potential energy goes on increasing, here it makes an angle 30∘to horizontal.
Due to its position it carries potential energy given by:
P.E=mgh, where m- mass of the rod, g- acceleration due to gravity, h – at the height the rod is pivoted.
Now, as we are calculating it in regard with the centre of mass,
We know that for a symmetric body it lies at the centre of a body. Thus, the centre of mass lies at a distance 2l as shown in the above figure.
So ‘h’ is calculated using trigonometry:
sin30∘=2lh∴h=2lsin30∘
Substituting this in (1), we get.
P.E=mg2lsin30∘sin30∘=21
∴P.E=mg4l …… (2)
Now when the rod is released then this potential energy is converted into rotational kinetic energy, given by,
K=21Iω2 ….. (3)
Where, I - is the moment of inertia of a rod =3ml2
ω - is the angular velocity.
Substituting for ‘I’ and equating (2) and (3), we get,
mg4l=213ml2ω2
Cancelling m and some numerical and taking ω on left hand side, we get
ω2=2l3g
Given that, g=10m/s2and l=50cm, substituting we get,
ω2=2×50×10−23×10
on solving we get,
ω2=30
⇒ω=30 rad s−1
Thus, the correct option is A.
Note: Students may make mistakes while calculating height h by taking length as ‘l’, but we are calculating potential energy w.r.t centre of mass so length is taken as l/2.
To solve these types of problems you have to remember the moment of inertia of an object, here M.I of rod is =3ml2.
