Question

A rod of length $20cm$ is made of metal. It expands by $0.075cm$ when the temperature is raised from ${0^o}C$ to ${100^o}C$ . Another rod of a different metal b having the same length expands by $0.045cm$for the same change temperature. A third rod of the same length is composed of two parts, one of metal $A$ and the other of metal $B$ . This rod expands by $0.060cm$ for the same change in temperature. The portion made of metal $A$ has the length
$\left( a \right)\,\,20cm$
$\left( b \right)\,\,10cm$
$\left( c \right)\,\,15cm$
$\left( d \right)\,\,18cm$

Answer 1

In the question we have to find the length of the rod $A$ which is a part of the third rod with $B$ . For that we have made use of the concept of linear expansion. Once we get the formula of linear expansion then we just have to find the missing values and by substituting then in the main equation we will get the length of the rod $A$ which is the part of the third rod with the composition of rod $B$ .

Complete Step by step solution:
Given that there is a rod of length 20cm which is made up of metal, it expands by $0.075cm$ when the temperature is raised from ${0^o}C$ to ${100^o}C$ . Also, there is a rod of different metal B having the same length which expands by $0.045cm$ with the same change in the temperature. There is also a third rod which is composed of other two metals $A$ and $B$ which expands by $0.060cm$ for the same amount of change in the temperature.
We have to find the length of the portion of the third rod which is made up of metal $A$ .
For this we will use the concept of linear expansion
Let the length of the third rod be $L$

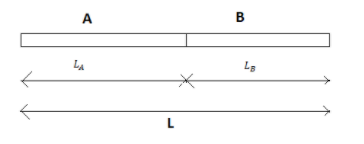
$\Rightarrow L = {L_A} + {L_B} = 20cm$
With the change in the temperature the change in the length of the third rod will be given by the equation $\vartriangle L = \vartriangle {L_A} + \vartriangle {L_B}$
Now, according to the linear expansion concept we can write
$\Rightarrow \vartriangle L = L\alpha \vartriangle T$
Similarly,
$\Rightarrow \vartriangle {L_A} = {L_A}{\alpha _A}\vartriangle T$ , and we will name it equation $1$
Also, we have
$\Rightarrow \vartriangle {L_B} = {L_B}{\alpha _B}\vartriangle T$ , and we will name it equation $2$
Now, by substitution in the above equitation we will get
$\Rightarrow \vartriangle L = {L_A}{\alpha _A}\vartriangle T + {L_{_B}}{\alpha _B}\vartriangle T$ , and we will name it equation $3$
Then we have to find the value of ${\alpha _A}$ and ${\alpha _B}$ for that we have to substitute the values in equation in $1$and $2$ then we will get
$\Rightarrow 0.075 = 20 \times {\alpha _A} \times 100$
Here, $\vartriangle T = {T_2} - {T_1}$ , $\vartriangle L = 0.075$ which is change in the length of the rod with the increase in temperature and ${L_A} = 20cm$
So, we will get the value of ${\alpha _A} = 3.75 \times {10^{ - 5}}$
Similarly, we can calculate the value of ${\alpha _B} = 2.25 \times {10^{ - 5}}$
Now substituting the value in equation $3$ we will get
$\Rightarrow 60 \times {10^{ - 3}} = \left( {{L_A} \times 3.75 \times {{10}^{ - 5}} \times 100} \right) + \left( {\left( {20 - {L_A}} \right) \times 2.25 \times {{10}^{ - 5}} \times 100} \right)$
On solving it more, we get
$\Rightarrow 60 = 1.5{L_A} + 45$
Solving for the constant value, we get
$\Rightarrow {L_A} = 10cm$
therefore, the value of ${L_A} = 10cm$

Therefore, the length of the rod $A$ in the third rod is $20cm$ .

Note: Remember the key formulas like formula of linear expansion then think how to approach this kind of question and after that try to find the missing values in the equation. These kinds of questions can sometimes be very hard to solve if one gets confused in the mid-way of solving the question. So, to avoid that try to solve step by step this will help in the future problem solving