Question

A rod of length 20 cm is made of metal. It expands by 0.075cm when its temperature is raised from $0{}^\circ C$to$100{}^\circ C$. Another rod of a different metal B having the same length expands by 0.045 cm for the same change in temperature. A third rod of the same length is composed of two parts, one of metal A and the other of metal B. This rod expands by 0.060 cm for the same change in temperature. The portion made of metal A has the length
A. 20 cm
B. 10 cm
C. 15 cm
D. 18 cm

Answer 1

Firstly, we will find the coefficient of thermal expansion of metals A and B using the suitable formula. Then, we will equate these values with that of the coefficient of thermal expansion of the composite metal (A plus B). Finally, upon continuing the calculation we will obtain the value of the portion made of the metal A.

Formula used:
$\dfrac{\Delta L}{L}={{\alpha }_{L}}\Delta T$

Complete answer:
The formula for computing the coefficient of the thermal expansion of metal is given as follows.

$\dfrac{\Delta L}{L}={{\alpha }_{L}}\Delta T$

Where L is the length of the metal, $\Delta L$is the change in the length of the metal, ${{\alpha }_{L}}$is the coefficient of thermal expansion of metal and $\Delta T$ is the change in the temperature.

Consider diagram:

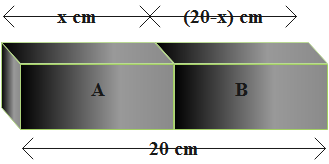
From given, we have the data as follows.

A rod of length $20 cm$ is made of metal. It expands by $0.075cm$ when its temperature is raised from $0{}^\circ C$to$100{}^\circ C$.

The coefficient of the thermal expansion of the metal A is given as follows.

$\dfrac{\Delta L}{L}={{\alpha }_{A}}\Delta T$

Substitute the given values in the above equation. So, we get,

$\dfrac{0.075}{20}={{\alpha }_{A}}(100-0)$

Continue further calculation.

${{\alpha }_{A}}=\dfrac{0.075}{20\times 100}$

B rod of length $20 cm$ is made of metal. It expands by $0.045cm$ when its temperature is raised from $0{}^\circ C$to$100{}^\circ C$.

The coefficient of the thermal expansion of the metal B is given as follows.

$\dfrac{\Delta L}{L}={{\alpha }_{B}}\Delta T$

Substitute the given values in the above equation. So, we get,

$\dfrac{0.045}{20}={{\alpha }_{B}}(100-0)$

Continue further calculation.

${{\alpha }_{B}}=\dfrac{0.045}{20\times 100}$

As, we have obtained the values of the coefficient of the thermal expansion of the metals A and B, thus, we will continue with the calculations of the composite metal expansion value.

Consider the figure while going through the following steps.

A composite rod of length $20 cm$ is made of metal. It expands by $0.06cm$ when its temperature is raised from $0{}^\circ C$to$100{}^\circ C$.

Let $x cm$ be the portion of the metal A and $(20 – x) cm$ be the portion of the metal B. So, we get,

$0.06=x\times {{\alpha }_{A}}\times 100+(20-x)\times {{\alpha }_{B}}\times 100$

Substitute the values of the coefficient of the thermal expansion of the metals A and B in the above equation.

& 0.06=x\times \dfrac{0.075}{20\times 100}\times 100+(20-x)\times \dfrac{0.045}{20\times 100}\times 100 \\\ & 0.06=x\times \dfrac{0.075}{20}+(20-x)\times \dfrac{0.045}{20} \\\ \end{aligned}$$ Continue the further calculation $$\begin{aligned} & 20\times 0.06=0.075x+20\times 0.045-0.045x \\\ & 1.2-0.9=x(0.075-0.045) \\\ & \Rightarrow 0.3=x0.03 \\\ \end{aligned}$$ Therefore, the value of $x$ is given as follows. $$\begin{aligned} & x=\dfrac{0.3}{0.03} \\\ & \Rightarrow x=10 \\\ \end{aligned}$$ $$\therefore $$ The portion made of metal A has the length of $10 cm$. **As the portion made of metal A has the length of $10 cm$, thus, the option (B) is correct.** **Note:** The units of the parameters should be taken care of, as in this case, the unit of the length in both the question statement and the options is given in terms of cm, so, no need to change. The unit conversion is must, if the question statement and the options have different forms of the units.