Question

A rod of length $2.4\;m$ and radius $4.6\;mm$ carries a negative charge of $4.2\times 10^{-7}\;C$ spread uniformly over its surface. The electric field near the midpoint of the rod, at a point on its surface is:
A. $-8.6 \times 10^5\;NC^{-1}$
B. $8.6 \times 10^4\;NC^{-1}$
C. $-6.7 \times 10^5\;NC^{-1}$
D. $6.7 \times 10^4\;NC^{-1}$

Answer 1

Begin by first establishing the angle between the electric field lines and the normal to the surface at the midpoint of the rod. Treat the rod as a cylinder and utilize Gauss’ Law that relates the electric flux through the surface of the rod and the charge on the rod. Remember that the electric flux can also be expressed in terms of the electric field and the normal to the surface area of the rod. Equate the two and rearrange the terms of the equation thus obtained to subsequently determine the electric field near the midpoint of the rod, which is what we require to this end.

Formula Used:
Electric field $E = \dfrac{q}{2\pi\epsilon_0 r L}$

Complete Solution:
Let us begin by understanding the term electric flux, following which we shall define and utilize Gauss’s law to solve the problem.

Electric flux is a qualitative measure of the number of electric field lines passing through a given surface. Note that electric field lines are a virtual illustration of the electric field strength and direction. Electric flux $\phi$ through a given surface $\vec{A}$ due to a uniform electric field $\vec{E}$ is given as:
$\phi=\vec{E}.\vec{A} = |\vec{E}||\vec{A}|cos\theta$, where $\theta$ is the angle between the electric field lines and the normal to the surface of area A.

Now, let us look at Gauss’ Law, which establishes a correlation between the electric flux and the electric charge. It states that the net electric flux through any closed surface is proportional to the total electric charge enclosed by that surface.
$\phi \propto q_{net} \Rightarrow \phi = \dfrac{1}{\epsilon_0}q_{net} = \dfrac{q_{net}}{\epsilon_0}$,
Where $\dfrac{1}{\epsilon_0}$ is introduced as a proportionality constant and $\epsilon_0 = 8.85\times 10^{-12}\;Fm^{-1}$ is the permittivity of electric field in free space/vacuum.

Now, let us look at the problem given to us:
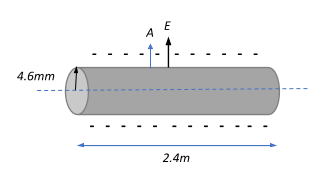
We have a rod of length $L = 2.4\;m$ and radius $r= 4.6\;mm = 4.6 \times 10^{-3}\;m$.
A charge of $q_{net} = -4.2\times 10^{-7}\;C$ is distributed uniformly over the surface.

Now, we consider the midpoint of the rod, which is on its curved surface. We see that the normal to the surface and the electric field (emanating ‘out’ from the surface, since field lines are directed ‘away’ from negative charges) are oriented in the same direction $(\theta = 0^{\circ})$.
Now, for a given surface, we have $\phi = |\vec{E}||\vec{A}|cos\theta$

Substituting that into the Gauss’ Law equation, we get:
$\phi = \dfrac{q_{net}}{\epsilon_0}$
$\Rightarrow |\vec{E}||\vec{A}|cos\theta = \dfrac{q_{net}}{\epsilon_0}$

Re-arranging the above equation after plugging in $\theta=0^{\circ} \Rightarrow cos0^{\circ} =1$ and $A=2\pi r L$:
$EA = \dfrac{q_{net}}{\epsilon_0} \Rightarrow E = \dfrac{q_{net}}{2\pi r L \epsilon_0}$

Plugging in our values, we get:
$E = \dfrac{-4.2\times10^{-7}}{2\times 3.14\times 4.6\times 10^{-3} \times 2.4 \times 8.85 \times 10^{-12} } =- 6.67 \times 10^{-7+12} = -6.67 \times 10^{5}\;NC^{-1}$

Therefore, the correct choice would be C. $-6.7 \times 10^{5}\;NC^{-1}$.

Note:
Remember that for any conductor, the net electric charge stored in a conductor resides entirely on its surface due to the mutual repulsion of like charges that demands such charges be as far apart as possible. This means that the electric field inside the conductor is zero, and the electric field at the surface of the conductor is perpendicular to that surface (as we’ve already seen in the problem).
Additionally, at the ends of the rod, we see that the angle between the electric field and the normal to the surface is $90^{\circ}$ which means that the net flux through the ends of the rod will be 0, since $\cos90^{\circ} = 0$. Thus, it is always important to be aware of the orientation of the field lines and the normal to the surface in flux-related calculations.