Question

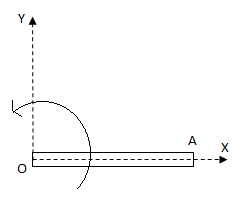
A rod of length 1m rotates in the xy plane about the fixed point O in the anticlockwise sense, as shown in the figure with velocity $\omega = a + bt$ where $a = 10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}$ and $b = 5\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 2}}}}$. The velocity and acceleration of the point A at $t = 0$ is

A. $+ 10\hat i\,{\text{m}}{{\text{s}}^{ - 1}}$ and $+ 5\hat i\,{\text{m}}{{\text{s}}^{ - 2}}$
B. $+ 10\hat j\,{\text{m}}{{\text{s}}^{ - 1}}$ and $\left( { - 100\hat i + 5\hat j} \right)\,{\text{m}}{{\text{s}}^{ - 2}}$
C. $+ 10\hat i\,{\text{m}}{{\text{s}}^{ - 1}}$ and $\left( {100\hat i + 5\hat j} \right)\,{\text{m}}{{\text{s}}^{ - 2}}$
D. $- 10\hat j\,{\text{m}}{{\text{s}}^{ - 1}}$ and $+ 5\hat i\,{\text{m}}{{\text{s}}^{ - 2}}$

Answer 1

Use the formula for linear velocity in terms of angular velocity. Since the particle is in rotational motion, it has centripetal and tangential acceleration. The direction of instantaneous velocity and tangential acceleration in circular motion is along the tangent and direction of centripetal acceleration is towards the centre.

Formula used:
The linear velocity $v$ of an object is
$v = R\omega$ …… (1)
Here, $R$ is the radius of the path and $\omega$ is the angular velocity.
The centripetal acceleration ${a_C}$ is given by
${a_C} = {\omega ^2}R$ …… (2)
Here, $\omega$ is the angular velocity and $R$ is the radius of the path.
The tangential acceleration ${a_t}$ is given by
${a_t} = R\alpha$ …… (3)
Here, $R$ is the radius of the path and $\alpha$ is the angular acceleration.

Complete step by step answer:
It is given that the length of the rod is $1\,{\text{m}}$.
We have given that the angular velocity is given by $\omega = a + bt$, where $a = 10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}$ and $b = 5\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 2}}}}$.
$\omega = a + bt$ …… (4)
The rod rotates about the point O. Hence, the radius of the circular path of the point A about point O is equal to the length of the rod.
$R = 1\,{\text{m}}$
Let us determine the angular velocity at time $t = 0$.
Substitute $10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}$ for $a$ and $0$ for $t$ in equation (4).
$\omega = \left( {10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}} \right) + b\left( 0 \right)$
$\Rightarrow \omega = 10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}$
Hence, the angular velocity at time $t = 0$ is $10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}$.

We can determine the linear velocity at point A at $t = 0$ using equation (1).
Substitute $1\,{\text{m}}$ for $R$ and $10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}$ for $\omega$ in equation (1).
$v = \left( {1\,{\text{m}}} \right)\left( {10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}} \right)$
$\Rightarrow v = 10\,{\text{m}} \cdot {{\text{s}}^{{\text{ - 1}}}}$
This velocity of the particle is in Y-direction.
Hence, the linear velocity at point A is $+ 10\hat j\,{\text{m}} \cdot {{\text{s}}^{{\text{ - 1}}}}$.

The angular acceleration is the rate of change of angular velocity with respect to time.
$\alpha = \dfrac{{d\omega }}{{dt}}$
Calculate the angular acceleration at point A using the above equation.
Substitute $a + bt$ for $\omega$ in the above equation.
$\alpha = \dfrac{{d\left( {a + bt} \right)}}{{dt}}$
$\Rightarrow \alpha = b$
Substitute $5\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 2}}}}$ for $b$ in the above equation.
$\Rightarrow \alpha = 5\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 2}}}}$
The particle is in rotational motion. Hence, it will have the centripetal and tangential components of acceleration.
The centripetal acceleration is towards point O, so has the negative X-direction. The tangential acceleration is in upward Y-direction.
The net acceleration is given by
$a = {a_C}\left( { - \hat i} \right) + {a_t}\hat j$
We can calculate the centripetal and tangential acceleration using equations (2) and (3).
Substitute ${\omega ^2}R$ for ${a_C}$ and for ${a_t}$ in the above equation.
$a = \left( {{\omega ^2}R} \right)\left( { - \hat i} \right) + \left( {R\alpha } \right)\hat j$
Substitute for $\omega$, for $R$ and $5\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 2}}}}$ for $\alpha$ in the above equation.
$a = \left( {{{\left( {10\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 1}}}}} \right)}^2}\left( {1\,{\text{m}}} \right)} \right)\left( { - \hat i} \right) + \left( {\left( {1\,{\text{m}}} \right)\left( {5\,{\text{rad}} \cdot {{\text{s}}^{{\text{ - 2}}}}} \right)} \right)\hat j$
$\Rightarrow a = \left( { - 10\hat i + 5\hat j} \right)\,{\text{m}} \cdot {{\text{s}}^{{\text{ - 2}}}}$
Hence, the acceleration at point A is $\left( { - 10\hat i + 5\hat j} \right)\,{\text{m}} \cdot {{\text{s}}^{{\text{ - 2}}}}$.
Hence, the velocity and acceleration at point A at $t = 0$ are $+ 10\hat j\,{\text{m}} \cdot {{\text{s}}^{{\text{ - 1}}}}$ and $\left( { - 10\hat i + 5\hat j} \right)\,{\text{m}} \cdot {{\text{s}}^{{\text{ - 2}}}}$ respectively.

So, the correct answer is “Option B”.

Note:
The students should keep in mind that the directions of the velocity and acceleration should be taken properly. The students may also try to determine the resultant of the tangential and centripetal acceleration to determine the acceleration at point A by taking their square and square root. But there is no need for such a lengthy process.