Question

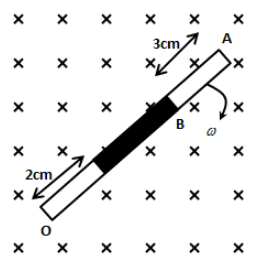
A rod of length 10cm made up of conducting and non-conducting material (shaded part is non-conducting). The rod is rotated with constant angular velocity 10 rad/s about point O, in constant magnetic field 2T as shown in figure. The induced emf between the point A and B of rod will be

A. 0.029 V
B. 0.1 V
C. 0.051 V
D. 0.064 V

Answer 1

Consider an elementary section of length of the rod at some distance from point O and calculate the motional emf induced in that small elementary section of the rod. Integrate the equation from point B to A, to determine the motional emf induced between A and B. you should use angular velocity rather than linear velocity of the rod in the formula for motional emf.

Formula used:
Motional emf, $\varepsilon = BvL$,
where, B is the magnetic field, v is the velocity and L is the length of the rod.

Complete step by step answer:
We have given that the length of the rod is $L = 10\,{\text{cm}}$, the angular velocity of rotation of rod is $\omega = 10\,{\text{rad/s}}$ and the magnetic field is $B = 2\,{\text{T}}$.Let us consider an elementary section of length of the rod at a distance r from O. As the rod starts rotating, due to motion of the rod, the motional emf will be induced in the rod. Let us express the motional emf induced by the elementary length of the rod placed in the uniform magnetic field as follows,
$d\varepsilon = Bvdr$
Here, B is the magnetic field, v is the velocity of the elementary length and $dr$is the small distance.

We know that, $v = r\omega$, where r is the radius of circular motion and $\omega$ is the angular velocity. Therefore, the above equation becomes,
$d\varepsilon = Br\omega dr$
Now, we can express the total induced emf between A and B by integrating the above equation within the limits ${r_i}$ to ${r_f}$.
$\int {d\varepsilon } = \varepsilon = \int\limits_{{r_i}}^{{r_f}} {Br\omega dr}$
$\Rightarrow \varepsilon = B\omega \int\limits_{{r_i}}^{{r_f}} {rdr}$
$\Rightarrow \varepsilon = B\omega \left( {\dfrac{{{r^2}}}{2}} \right)_{{r_i}}^{{r_f}}$

Now, $OB = {r_i} = 0.1 - 0.03 = 0.07\,{\text{m}}$ and $OA = {r_f} = 0.1\,{\text{m}}$.
Substituting $B = 2\,{\text{T}}$, $\omega = 10\,{\text{rad/s}}$, ${r_i} = 0.07\,{\text{m}}$ and ${r_f} = 0.1\,{\text{m}}$ in the above equation, we get,
$\varepsilon = \left( 2 \right)\left( {10} \right)\left( {\dfrac{{{r^2}}}{2}} \right)_{0.07}^{0.1}$
$\Rightarrow \varepsilon = \left( {20} \right)\left( {\dfrac{{{{\left( {0.1} \right)}^2}}}{2} - \dfrac{{{{\left( {0.07} \right)}^2}}}{2}} \right)$
$\Rightarrow \varepsilon = \left( {20} \right)\left( {2.55 \times {{10}^{ - 3}}} \right)$
$\therefore \varepsilon = 0.051\,{\text{V}}$

So, the correct answer is option C.

Note: The linear velocity of the particles of the rod is different at different positions from point O. But, the angular velocity is the same for each particle since it deals with revolutions per unit time. In the solution, we have determined the emf induced in the small elementary length of the rod and to calculate the total emf induced, we have simply integrated the small emf equation. While determining the motional emf, the value of magnetic field should be constant that is uniform magnetic field.