Question

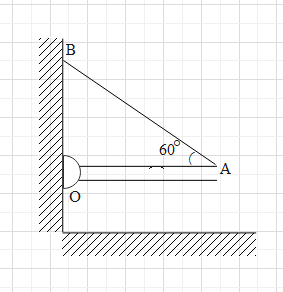
A rod OA of mass 4kg is held in a horizontal position by a massless string AB as shown in figure. Length of the rod is 2m. Find net force exerted by hinge on the rod. (g= 10m/$s^2$)

A. 23.1N
B. 20N
C. 17.32N
D. 14.14N

Answer 1

For this question we will use the vector components. The vector component helps in formulation of the equation to calculate the force exerted on the road. Free diagram is helpful in breaking the components. The values given in the question are then substituted in the equation formed.

Complete step-by-step answer:
A rod of mass m is held by a string. The length of rod is l. We have to find the net force exerted by hinge.
Given

& m=4kg \\\ & l=2m \\\ & \theta =60{}^\circ \\\ \end{aligned}$$ Below is the free body diagram of a rod inclined at an angle. The vertical, horizontal and normal components have been labeled properly. The horizontal component is $$T\cos \theta $$ and the vertical component is $$T\sin \theta $$.  Let us consider that T be the tension on the rod acting at an angle $$60{}^\circ $$ and N be the normal force acting on the rod. Now we have to balance forces to calculate the force exerted. On resolving the components, the horizontal component will be equal to mg and the vertical component will be equal to the normal force N. Below is the equation formed by the components- $$\begin{aligned} & T\sin \theta =mg \\\ & T\cos \theta =N \\\ \end{aligned}$$ Now substituting the given value in above equation we get $$\begin{aligned} & N=\dfrac{40}{1.73} \\\ & =23.1N \end{aligned}$$ Therefore the total force exerted by the rod is found to be 23.1N. **So, the correct answer is “Option A”.** **Note:** Free body diagram is made for better understanding of components. Free body diagram helps to break the vector into its component. The vertical and horizontal components should be placed carefully with their normal components otherwise the entire solution will go wrong.