Question
Question: A rod leans against a stationary cylindrical body as shown in figure, and its right end slides to th...
A rod leans against a stationary cylindrical body as shown in figure, and its right end slides to the right on the floor with a constant speed v. Choose the correct options:
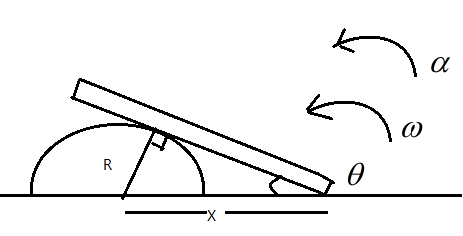
Solution
To begin with let us understand the definition of angular acceleration and angular velocity, first. These are often seen in bodies which undergo rotation.
We know that angular velocity ω is defined as the rate at which the angular position varies with respect to time, and also given as ω=rv where v is the linear velocity and r is the from between the centre of the circle and the position of the body. Whereas, angular acceleration α is the change in angular velocity with respect to time.
Formula used:
ω=−dtdθ andα=dtdω
Complete step-by-step answer:
Let us assume that the radius of the cylindrical body is R, and that the rod makes an angle θ with the ground. Let the distance between the centre of the cylinder and the point where the rod touches the ground be X, and let the rod move with a linear velocity v, angular velocity ω and experience and angular acceleration α as shown in the figure.
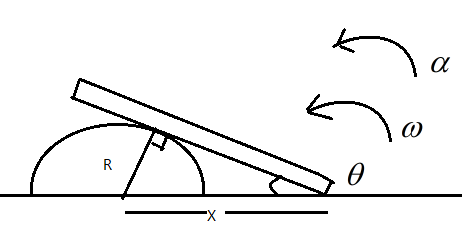
Clearly, from the diagram we can say that sinθ=XR, rearranging, we get X=sinθR
Then we know that linear velocity of rod v can be expressed as v=dtdx.
Then, we have v=dtd(sinθR)=sin2θ−Rcosθ(dtdθ)
But we know also know that angular accelerationω is given as ω=−dtdθ
Then substituting the value of ωin v, we get,
v=sin2θRcosθω
Rearranging, we get ω=Rcosθvsin2θ
From sin2θ+cos2θ=1, we can write cosθ=1−sin2θ
Replacing, we get, ω=R1−sin2θvsin2θ
Substituting for sinθ as sinθ=XR, we get, ω=R1−(XR)2v(XR)2=xx2−R2Rv
Hence we get ω=xx2−R2Rv
We also know that angular acceleration α is given asα=dtdω
Then differentiating ω with respect to t we get, α=(x(x2−R2))2−Rv[x2−R2+2x2−R2x.2x]=x2(x2−R2)23−Rv[x2−R2+x2]=x2(x2−R2)23−Rv(2x2−R2)
Hence we get α=x2(x2−R2)23−Rv(2x2−R2)
Thus the answer is
