Question

A rod is bent into a semi-circular arc of radius R. The rod has a uniform linear charge distribution $\lambda$ . The potential at the center of arc, point P is:
(A) $\dfrac{\lambda }{{2\pi {\varepsilon _o}R}}$
(B) $\dfrac{\lambda }{{4{\varepsilon _o}}}$
(C) $\dfrac{\lambda }{{2{\varepsilon _o}}}$
(D) $\dfrac{\lambda }{{{\varepsilon _o}}}$

Answer 1

In order to solve this question we will consider an elementary width and due to it we will find the potential at the center of the arc and in order to find it we will have to integrate it and we will get the required potential at the center of the arc.

Complete step by step solution:

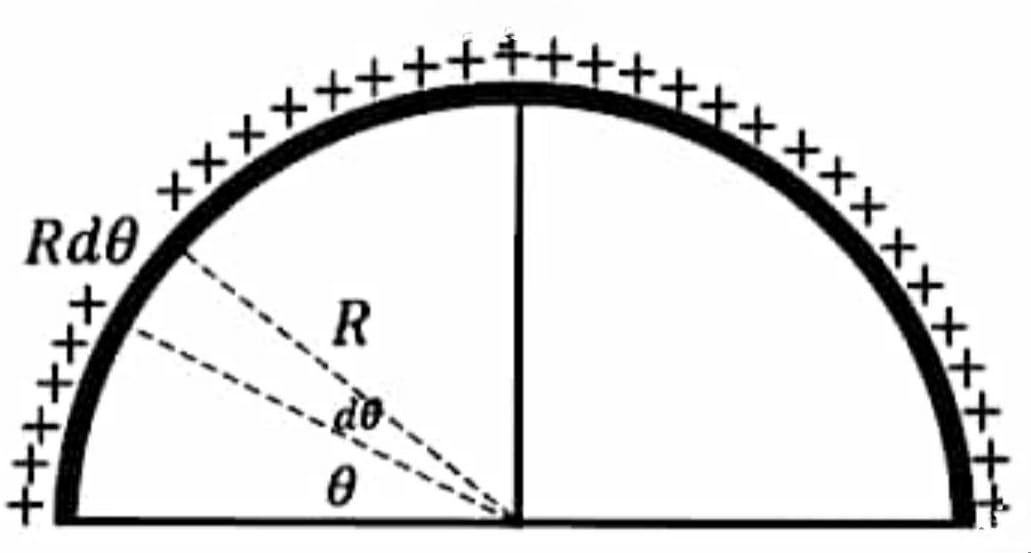
For solving this question we have to consider elementary width $dx$ and we will find the elementary charge present on it;
Since the linier charge density is given as $\lambda$ or mathematically we can write it as:
$\lambda = \dfrac{Q}{L}$
Since it is a semicircular arc so $L = \pi R$ now putting this value in place of L:
$\lambda = \dfrac{Q}{{\pi R}}$
After substituting it we will get the equation of elementary charge as:
$dq = \lambda dx$
Putting the value of $\lambda$ in this equation;
$dq = \dfrac{Q}{{\pi R}}dx$
Now the potential energy at point P will be
$\int {d{V_1} = \int {\dfrac{{Kdq}}{R}} }$
Putting the value of $dq$ in this equation:
$\int {d{V_1} = \int {\dfrac{{KQdx}}{{R\pi R}}} }$
Since we have considered the constant K so it can be removed by putting the limits;
${V_p} = \int\limits_0^{\pi R} {\dfrac{Q}{{\pi R}} \times \dfrac{{dx}}{{4\pi {\varepsilon _o}R}}}$
On integrating we get:
${V_p} = \dfrac{Q}{{4\pi {\varepsilon _o}R}}$
Pitting the value of Q in terms of charge density $\lambda$
${V_p} = \dfrac{{\lambda \times \pi R}}{{4\pi {\varepsilon _o}R}}$
On further solving we get:
${V_p} = \dfrac{\lambda }{{4{\varepsilon _o}}}$
Hence the correct option is B.

Note:
While solving these types of problems we should be very careful in consideration of the elementary width because this is the base of the whole question. If this is wrong then the whole process and the answer will be wrong. One thing can also be remembered that the electric field due to semicircular ring will be $\dfrac{\lambda }{{2\pi {\varepsilon _o}R}}$