Question
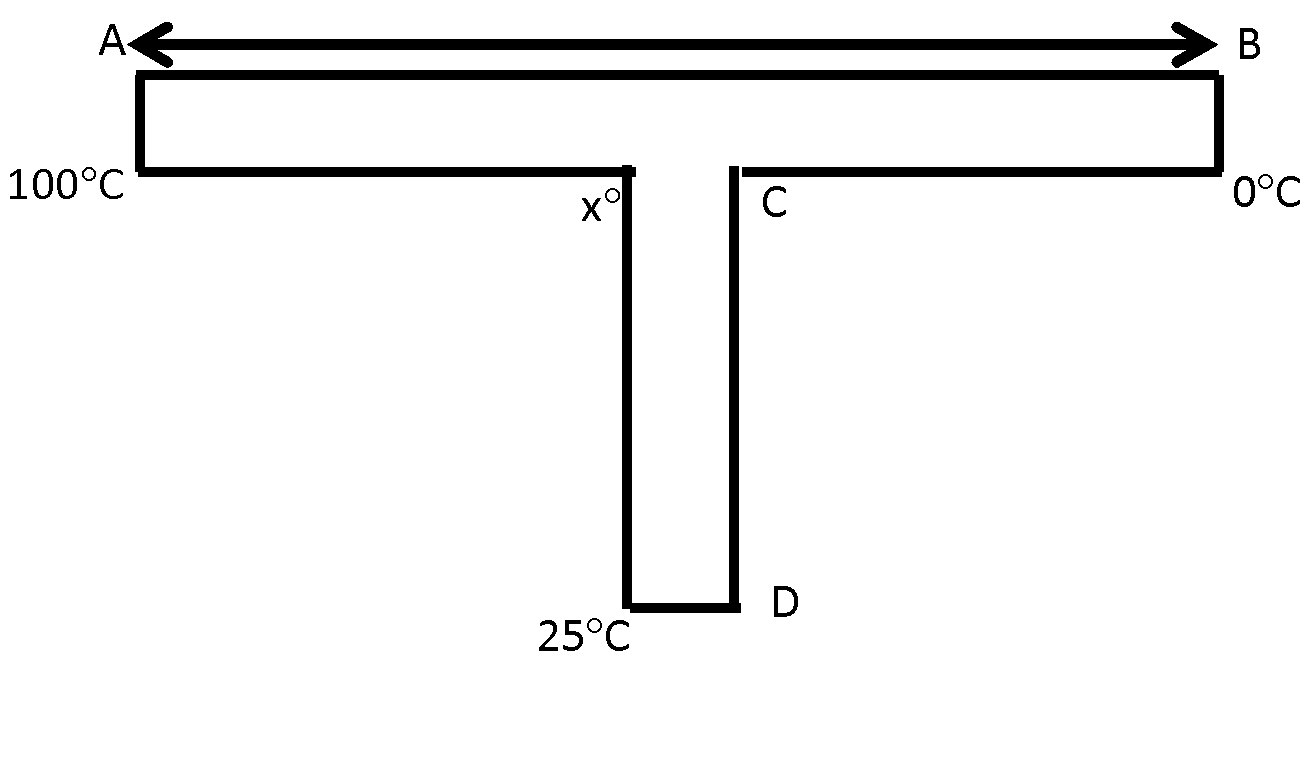
Question: A rod CD of thermal resistance \(5.0K/W\) is joined at the middle of an identical rod AB as shown in...
A rod CD of thermal resistance 5.0K/W is joined at the middle of an identical rod AB as shown in figure, the ends A, B and D are maintained at 10∘C and 25∘C respectively. Find the heat current (in W) in CD.
Solution
The heat current always flows from higher temperature to lower temperature. Also, by junction law, the heat current through AC is the sum of heat current through CD and CB.
Formula used:
Heat current, H=tQ=xKA(T1−T2)
Where A is the cross sectional area T1 is the temperature of the hot part.
T2 is temperature of cold part
x is the length covered
Q is heat and t is time taken for its flow
Complete step by step answer:
As both rods are identical, so the areas of both are same
And total lengths are also the same. So, area of cross section is
constant =A. As A is at higher temperature than both
D and B So, current will flow from A to both arms B and D.
So, by junction law, heat current of AC = Heat current of BC + Heat current of CD
i.e.,
HAC=HCB+HCD… (i)
Let C be at x∘C temperature.
as we know heat current, H=xKA(T1−T2)
So, equation (i) becomes
l/2KA(100−x)=l/2KA(x−0)+lKA(x−25)
⇒2(100−x)=2(x)+x−25 ⇒200−2x=2x+x−25 ⇒200−2x=3x−25 ⇒5x=225 ⇒x=5225 ⇒x=45∘C
So, the temperature at C is 45∘C.
So, the heat current for part CD is
HCD=tQ=lKA(45−25) =l/KA20=520=4W
As thermal resistance =KAl=5KW−1
So, heat current is 4W.
Note:
Remember for heat currents HAC and HCB, the value of x is l/2 not l this is because the rod CD is in the middle of AB.Also remember the concept of thermal resistance and calorimetry while solving the question.
