Question

A rod AC of length Landmass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of the same mass m moving with velocity v strikes rod at point B which is at a distance L/4 from midpoint making angle ${37^0}$ with the rod. The collision is elastic. After collision

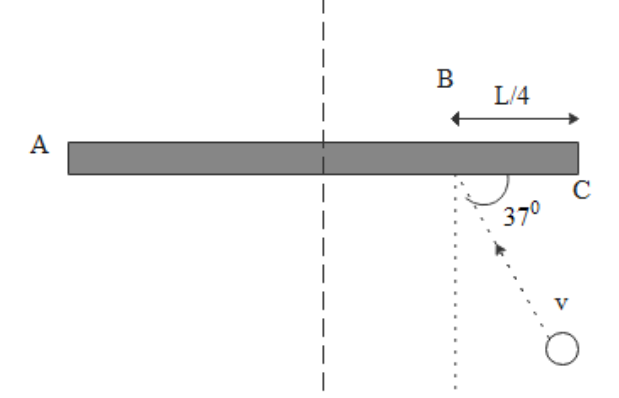
A. angular velocity of the rod will be $\dfrac{{72v}}{{55L}}$
B. The center of the rod will travel a distance $\dfrac{{\pi L}}{3}$ in the time in which it makes a half rotation
C. impulse of the impact force is $\dfrac{{24mv}}{{55}}$
D. none of these

Answer 1

These kind of collision questions to be solved by assuming the ball and rod as a system because there will be no external force and we can conserve the linear momentum of the system. Since the rod is free to rotate there will be angular velocity too and we should solve for it.
Formula used:
\eqalign{ & p = mv \cr & L = mvr \cr & L = I\omega \cr & \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}} = 1 \cr}

Complete step-by-step solution:
Since the ball is hit at the rod, exactly at the point of collision and along the normal to the rod we can apply the coefficient of restitution equation.
After hitting, let the rod rotate with $\omega$ angular velocity and translate with ‘u’ velocity and the ball moves with ${v^1}$ velocity after collision.
Now let us consider the ball as body 1 and the rod as body 2.

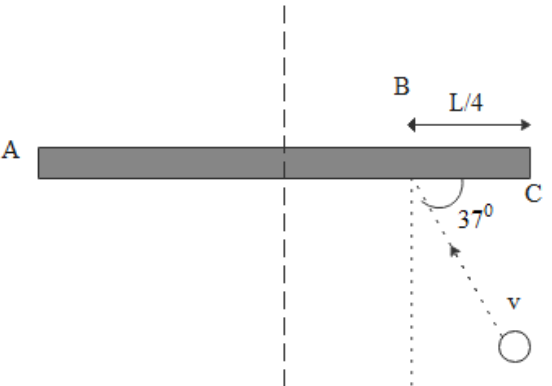
For elastic collision we have
$\dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}} = 1$
\eqalign{ & \Rightarrow {u_1} = v\sin {37^0} = \dfrac{{3v}}{5} \cr & \Rightarrow {v_2} = {v_{com}} + r\omega = u + \dfrac{{\omega L}}{4} \cr & \Rightarrow {v_1} = - {v^1} \cr}
By substituting all in above restitution equation we get
$\dfrac{{3v}}{5} = \left( {u + \dfrac{{\omega L}}{4}} \right) + {v^1}$ ...............…eq 1
Now we will conserve the linear momentum of rod and ball system perpendicular to rod.
We have linear momentum as product of mass and velocity $p = mv$
Using this we get
$\dfrac{{3mv}}{5} = \left( {mu} \right) - m{v^1}$ .....……………. eq 2
Now we will conserve angular momentum of the rod about the point of hitting.
Angular momentum for translation will be $L = mvr$ and for rotation will be $L = I\omega$
Initial angular momentum of the system is zero and after collision only the rod will have both translational and rotational angular momentum and it rotates about the center of mass of the rod. Moment of inertia of rod about center of mass will be $I = \dfrac{{m{L^2}}}{{12}}$
From angular momentum conservation about point of hitting we have
$0 = 0 + \left( {\dfrac{{muL}}{4} - \dfrac{{m{L^2}\omega }}{{12}}} \right)$ .........… eq 3
By solving equation 1 and 2 and 3 we get $u = \dfrac{{24v}}{{55}},\omega = \dfrac{{72v}}{{55L}}$
Time taken for half rotation means for rotating $\pi$ radians will be $t = \dfrac{\pi }{\omega }$
In this time interval center of mass of rod will travel $s = ut = u\dfrac{\pi }{\omega } = \dfrac{{\pi L}}{3}$
Impulse on rod is magnitude of final linear momentum of rod – initial linear momentum of rod which will be
\eqalign{ & \dfrac{{24mv}}{{55}} - 0 \cr & \Rightarrow \dfrac{{24mv}}{{55}} \cr}
Hence
Angular velocity of the rod is $\dfrac{{72v}}{{55L}}$ and the centre of the rod travelled a distance $\dfrac{{\pi L}}{3}$ in the time in which it makes half rotation and impulse of the impact force is $\dfrac{{24mv}}{{55}}$
So option A and option B and option C three are correct.

Note: In case of conservation of angular momentum we can conserve about the point of hitting or about the center of mass of rod because in both the cases torque acting will be zero which is the essential condition for conserving the angular momentum.